Introduction to Difference in Differences

ECON526

Paul Schrimpf

University of British Columbia

Introduction

Context:
- Have a policy applied to some observations but not others, and observe outcome before and after policy
Idea:
- Compare outcome before and after policy in treated and untreated group
Change in outcome in treated group reflects both effect of policy and time trend, change in untreated group captures time trend

Example: Impact of Billboards

From Facure (2022) chapter 13
Bank placed billboards advertising savings accounts in Porto Alegre in July
Data on deposits in May and July in Porto Alegre and Florianopolis

Example: Impact of Billboards

Code

import warnings
warnings.filterwarnings('ignore')
import pandas as pd
from matplotlib import pyplot as plt
import statsmodels.formula.api as smf

datadir="./data"

data = pd.read_csv(datadir + "/billboard_impact.csv")
data.head()

	deposits	poa
0	42	1
1	0	1
2	52	1
3	119	1
4	21	1

Means and Differences

tbl = data.groupby(['jul','poa']).mean().unstack()
tbl

	deposits
poa	0	1
jul
0	171.642308	46.01600
1	206.165500	87.06375

tbl.diff(axis=0).iloc[1,:]

          poa
deposits  0      34.523192
          1      41.047750
Name: 1, dtype: float64

tbl.diff(axis=1).iloc[:,1]

jul
0   -125.626308
1   -119.101750
Name: (deposits, 1), dtype: float64

tbl.diff(axis=0).diff(axis=1).iloc[1,1]

np.float64(6.524557692307688)

Difference in Differences

\[ % \def\Er{{\mathrm{E}}} \def\En{{\mathbb{E}_n}} \def\cov{{\mathrm{Cov}}} \def\var{{\mathrm{Var}}} \def\R{{\mathbb{R}}} \newcommand\norm[1]{\left\lVert#1\right\rVert} \def\rank{{\mathrm{rank}}} \newcommand{\inpr}{ \overset{p^*_{\scriptscriptstyle n}}{\longrightarrow}} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \]

Setup

Two periods, binary treatment in second period
Potential outcomes \(\{y_{it}(0),y_{it}(1)\}_{t=0}^1\) for \(i=1,...,N\)
Treatment \(D_{it} \in \{0,1\}\),
- \(D_{i0} = 0\) \(\forall i\)
- \(D_{i1} = 1\) for some, \(0\) for others
Observe \(y_{it} = y_{it}(0)(1-D_{it}) + D_{it} y_{it}(1)\)

Identification

Average treatment effect on the treated:

\[ % \begin{align*} ATT & = \Er[y_{i1}(1) - \color{red}{y_{i1}(0)} | D_{i1} = 1] \\ & = \Er[y_{i1}(1) - y_{i0}(0) | D_{i1} = 1] - \Er[\color{red}{y_{i1}(0)} - y_{i0}(0) | D_{i1}=1] \\ & \text{ assume } \Er[\color{red}{y_{i1}(0)} - y_{i0}(0) | D_{i1}=1] = \Er[y_{i1}(0) - y_{i0}(0) | D_{i1}=0] \\ & = \Er[y_{i1}(1) - y_{i0}(0) | D_{i1} = 1] - \Er[y_{i1}(0) - y_{i0}(0) | D_{i1}=0] \\ & = \Er[y_{i1} - y_{i0} | D_{i1}=1, D_{i0}=0] - \Er[y_{i1} - y_{i0} | D_{i1}=0, D_{i0}=0] \end{align*} \]

Important Assumptions

No anticipation: \(D_{i1}=1\) does not affect \(y_{i0}\)
- built into the potential outcomes notation we used
- could relax by allowing potential outcomes given sequence of \(D\), i.e. \(y_{it}(D_{i0},D_{i1})\), but then need different assumptions and estimator
Parallel trends: \(\Er[\color{red}{y_{i1}(0)} - y_{i0}(0) |D_{i1}=1,D_{i0}=0] = \Er[y_{i1}(0) - y_{i0}(0) | D_{i1}=0, D_{i0}=0]\)
- not invariant to tranformations of \(y\)

Estimation

Plugin: \[ % \widehat{ATT} = \frac{ \sum_{i=1}^n (y_{i1} - y_{i0})D_{i1}(1-D_{i0})}{\sum_{i=1}^n D_{i1}(1-D_{i0})} - \frac{ \sum_{i=1}^n (y_{i1} - y_{i0})(1-D_{i1})(1-D_{i0})}{\sum_{i=1}^n (1-D_{i1})(1-D_{i0})} \]
Regression: \[ % y_{it} = \delta_t + \alpha 1\{D_{i1}=1\} + \beta D_{it} + \epsilon_{it} \] then \(\hat{\beta} = \widehat{ATT}\)

Billboard Application Revisited

Visualizing Difference in Differences

poa_before = data.query("poa==1 & jul==0")["deposits"].mean()
poa_after = data.query("poa==1 & jul==1")["deposits"].mean()
fl_before = data.query("poa==0 & jul==0")["deposits"].mean()
fl_after = data.query("poa==0 & jul==1")["deposits"].mean()
plt.figure(figsize=(10,5))
plt.plot(["May", "Jul"], [fl_before, fl_after], label="FL", lw=2)
plt.plot(["May", "Jul"], [poa_before, poa_after], label="POA", lw=2)

plt.plot(["May", "Jul"], [poa_before, poa_before+(fl_after-fl_before)],
         label="Counterfactual", lw=2, color="C2", ls="-.")

plt.legend();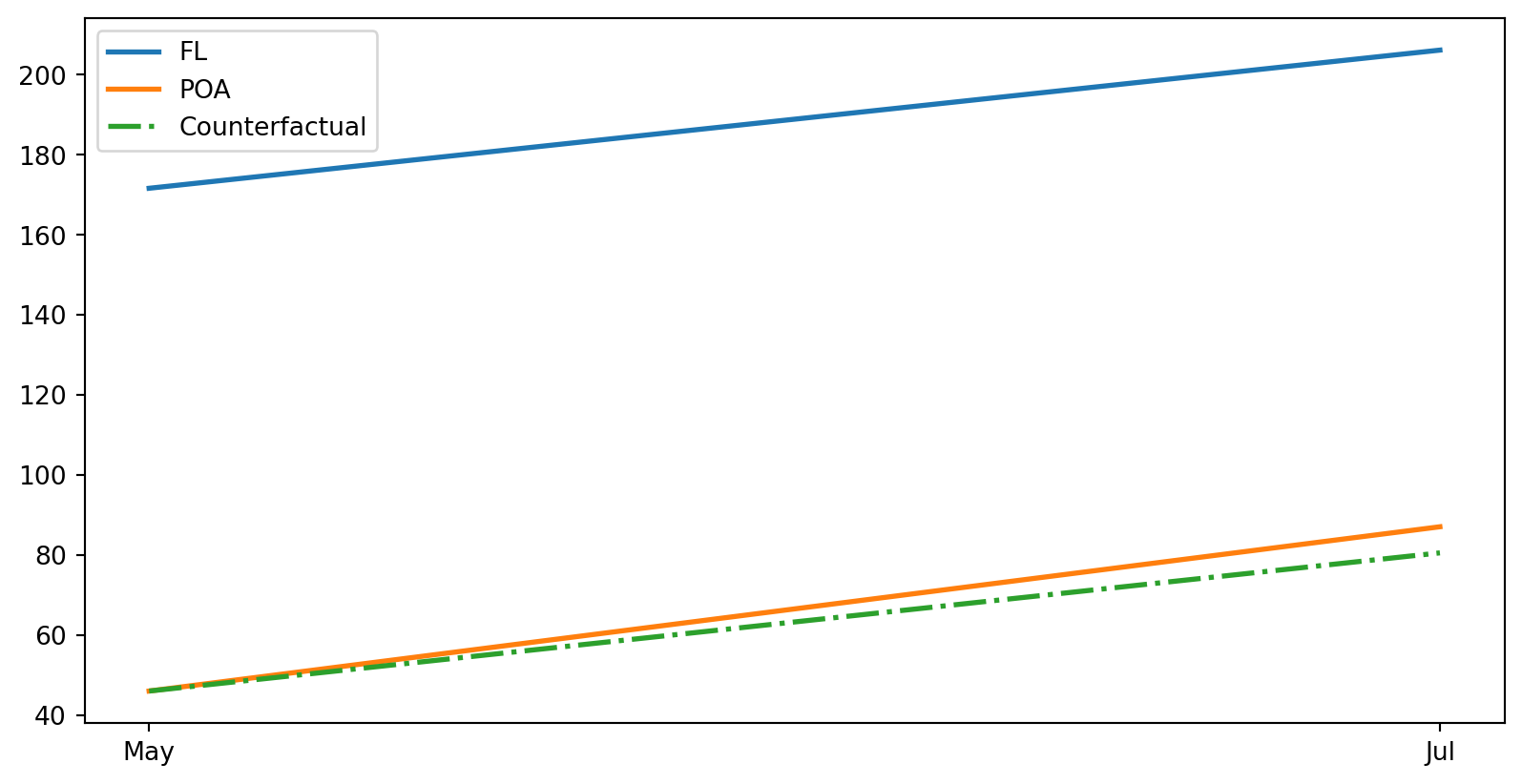

Estimation via Regression

from statsmodels.iolib.summary2 import summary_col
summary_col(smf.ols('deposits ~ poa*jul', data=data).fit(cov_type="HC3"))

	deposits
Intercept	171.6423
	(2.4989)
poa	-125.6263
	(3.0774)
jul	34.5232
	(3.3431)
poa:jul	6.5246
	(4.2478)
R-squared	0.3126
R-squared Adj.	0.3122

Standard errors in parentheses.

Parallel Trends and Functional Form

Parallel trends for an outcome does not imply parallel trends for functions of it
- For example, \[ \Er[\color{red}{y_{i1}(0)} - y_{i0}(0) |D_{i1}=1,D_{i0}=0] = \Er[y_{i1}(0) - y_{i0}(0) | D_{i1}=0, D_{i0}=0] \] does not imply \[ \Er[\log \color{red}{y_{i1}(0)} - \log y_{i0}(0) |D_{i1}=1,D_{i0}=0] = \Er[\log y_{i1}(0) - \log y_{i0}(0) | D_{i1}=0, D_{i0}=0] \]

Parallel Trends in Logs

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Parameters
n_periods = 5
n_groups = 2
group_names = ['Control', 'Treatment']

time = np.arange(n_periods)
group = np.array([0, 1])  # 0: Control, 1: Treatment

intercepts = [1, 5]  # Different starting points
trend = 1  # Same trend for both groups

# Simulate outcomes
data = []
for g in group:
    for t in time:
        y = intercepts[g] + trend * t #+ np.random.normal(0,1)
        data.append({'group': group_names[g], 'time': t, 'y': y})

df = pd.DataFrame(data)
df['log_y'] = np.log(df['y'])

# Plot levels
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
for name, grp in df.groupby('group'):
    plt.plot(grp['time'], grp['y'], label=name)
plt.title('Outcome in Levels')
plt.xlabel('Time')
plt.ylabel('y')
plt.legend()

# Plot logs
plt.subplot(1,2,2)
for name, grp in df.groupby('group'):
    plt.plot(grp['time'], grp['log_y'], label=name)
plt.title('Outcome in Logs')
plt.xlabel('Time')
plt.ylabel('log(y)')
plt.legend()

plt.tight_layout()
plt.show()

Parallel Trends in Logs

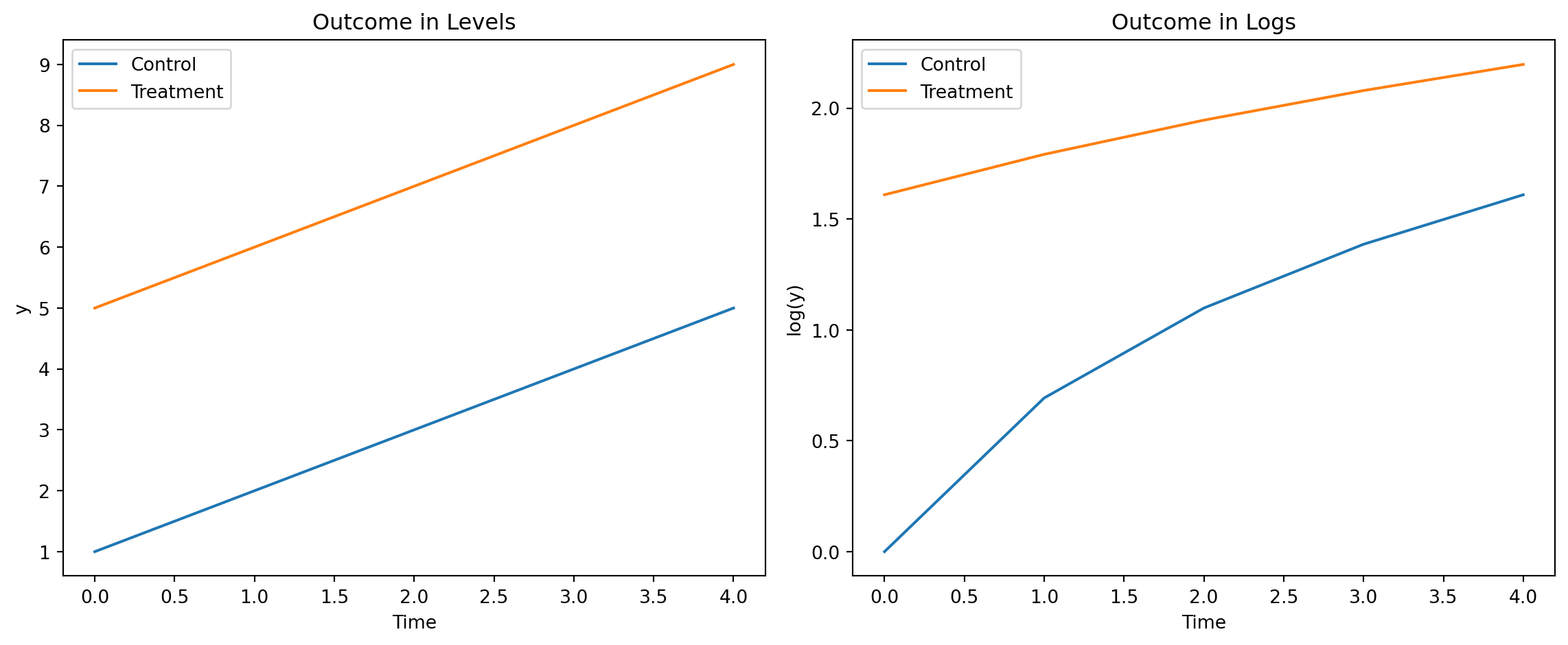
Parallel Trends in Growth Rates

# Parameters
n_periods = 10
group_names = ['Control', 'Treatment']
initials = [10, 9]  # Different starting values
growth = [1.10, 1.07]
growth_trend = -0.005

# Simulate outcomes
data = []
for g, initial in enumerate(initials):
    y = initials[g]
    for t in range(n_periods):
        data.append({'group': group_names[g], 'time': t, 'y': y})
        y *= growth[g] + growth_trend * t

df = pd.DataFrame(data)
df['log_y'] = np.log(df['y'])

# Compute growth rates (difference in logs)
df['growth_rate'] = df.groupby('group')['log_y'].diff()

# Plot levels
plt.figure(figsize=(15,4))
plt.subplot(1,3,1)
for name, grp in df.groupby('group'):
    plt.plot(grp['time'], grp['y'], label=name)
plt.title('Outcome in Levels')
plt.xlabel('Time')
plt.ylabel('y')
plt.legend()

# Plot logs
plt.subplot(1,3,2)
for name, grp in df.groupby('group'):
    plt.plot(grp['time'], grp['log_y'], label=name)
plt.title('Outcome in Logs')
plt.xlabel('Time')
plt.ylabel('log(y)')
plt.legend()

# Plot growth rates
plt.subplot(1,3,3)
for name, grp in df.groupby('group'):
    plt.plot(grp['time'], grp['growth_rate'], label=name)
plt.title('Growth Rates (Δlog(y))')
plt.xlabel('Time')
plt.ylabel('Growth Rate')
plt.legend()

plt.tight_layout()
plt.show()

Parallel Trends in Growth Rates

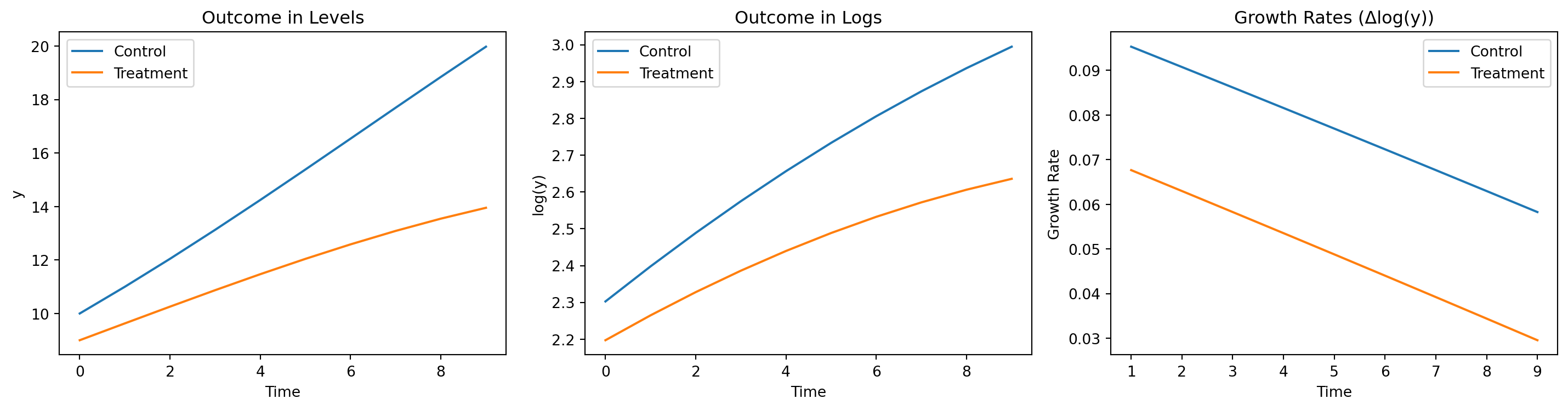
Further Topics

More periods, more groups
Covariates
Pre-trends

Reading

Chapter 13 of Facure (2022)

References

Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.