Instrumental Variables

ECON526

Paul Schrimpf

University of British Columbia

Introduction

\[ \def\indep{\perp\!\!\!\perp} % \def\idp{\perp\kern-5pt\perp} \def\Er{\mathrm{E}} \def\var{\mathrm{Var}} \def\cov{\mathrm{Cov}} \def\R{\mathbb{R}} \def\En{{\mathbb{E}_n}} \def\Pr{\mathrm{P}} \newcommand{\norm}[1]{\left\Vert {#1} \right\Vert} \newcommand{\abs}[1]{\left\vert {#1} \right\vert} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]

Endogeneity

\[ Y_i = X_i' \beta_0 + \epsilon_i \]

Believe \(\Er[X_i \epsilon_i] \neq 0\), so OLS biased and inconsistent

Sources of Endogeneity

Omitted variables
Simultaneity
Measurement error
And more …

Omitted Variables

Desired model \[ Y_i = X_i'\beta_0 + W_i'\gamma_0 + \epsilon_i \] Assume \(\Er[\epsilon] = \Er[X\epsilon] = \Er[W\epsilon] = 0\)
Estimated model \[ Y_i = X_i'\beta + \underbrace{u_i}_{\equiv W_i'\gamma_0 + \epsilon_i} \]

Omitted Variables Bias

OLS inconsistent and biased

\[ \plim \hat{\beta}^{OLS} \inprob \beta_0 + \Er[X_i X_i']^{-1} \Er[X_i W_i'] \gamma_0 \]

Or if \(X_i = (1, x_i)'\) and \(W_i\) is a scalar, \(y_i = \beta_0 + \beta_1 x_i + \gamma_0 w_i + \epsilon\) \[ \plim \hat{\beta}_1 \inprob \beta_1 + \frac{\cov(x_i,w_i)}{\var(x_i)} \gamma_0 \]

Simultaneity

Equilibrium conditions lead to variables that are simultaneously determined
Demand and supply: \[ \begin{align*} Q_i^D & = P_i \beta_D + X_D'\gamma_D + u_{D,i} \\ Q_i^S & = P_i \beta_S + X_S'\gamma_S + u_{S,i} \\ Q_i^S & = Q_i^D \end{align*} \]
Assume \(X_D\) and \(X_S\) exogenous
- \(0 = \Er[X_D u_{D,i}] = \Er[X_D u_{S,i}] = \Er[X_S u_{D,i}] = \Er[X_S u_{S,i}]\)

Simultaneity

Structural equations: (demand and inverse supply): \[ \begin{align*} Q_i & = P_i \beta_D + X_D'\gamma_D + u_{D,i} \\ P_i & = Q_i \frac{1}{\beta_S} - X_S'\gamma_D\frac{1}{\beta_S} - u_{S,i}\frac{1}{\beta_S} \\ \end{align*} \]
Reduced form: \[ \begin{align*} Q_i = & \frac{\beta_D}{\beta_D - \beta_S} \left( -X_{D,i}' \gamma_D + X_{S,i}'\gamma_S - u_{D,i} + u_{S,i} \right) + X_{D,i}'\gamma_D + u_{D,i} \\ P_i = & \frac{1}{\beta_D - \beta_S}\left(-X_{D,i}' \gamma_D + X_{S,i}'\gamma_S - u_{D,i} + u_{S,i} \right) \end{align*} \]
\(\Er[P_i u_{D,i}] \neq 0\), so OLS estimate of \(Q_i = P_i \beta_D + X_D'\gamma_D + u_{D,i}\) is biased and inconsistent

Measurment Error

True model \[ Y_i = \beta_0 + \beta_1 x_i^* + \epsilon_i \] with \(\Er[x_i^* \epsilon_i]=0\), but \(x_i^*\) unobserved
Observe \(x_i = x_i^* + u_i\)
Estimated model \[ Y_i = \beta_0 + \beta_1 x_i + \underbrace{\tilde{\epsilon}_i}_{\equiv -\beta_1 u_i + \epsilon_i} \]
\(\Er[x_i\tilde{\epsilon}_i] = -\beta_1\Er[u_i^2] \neq 0\)

Instrumental Variables

\[ Y_i = \underbrace{X_i}_{\in \R^k}' \beta_0 + \epsilon_i \]

\(\Er[\epsilon_i] = 0\), but \(\Er[X_i \epsilon_i] \neq 0\)
Instrument \(Z_i \in \R^d\) s.t.
1. Relevant \(rank(\Er[Z_i X_i']) = k\)
2. Exogenous \(\Er[Z_i \epsilon_i] = 0\)

Code

import graphviz as gr

dot = gr.Digraph()
dot.edge('X', 'Y', style = 'dashed')
dot.edge('ϵ','Y')
dot.edge('ϵ','X')
dot.edge('Z','X')
dot

Instrumental Variables Estimator

Assumed \(0 = \Er[Z_i \epsilon_i] = \Er[Z_i(y_i - X_i'\beta_0)]\)
Estimate by solving \[ 0 \approx \frac{1}{n} \sum_{i=1}^n Z_i(y_i - X_i'\hat{\beta}^{2SLS}) \]
\(\hat{\beta}^{2SLS} = (X'Z (Z'Z)^{-1} Z' X)^{-1} (X'Z(Z'Z)^{-1}Z'y)\)

Two Stage Least Squares

\[ \begin{align*} \hat{\beta}^{2SLS} & = (X'Z (Z'Z)^{-1} Z' X)^{-1} (X'Z(Z'Z)^{-1}Z'y) \\ & = (X'P_Z X)^{-1} (X' P_Z y) \\ & = ((P_Z X)'(P_Z X))^{-1} ((P_Z X)'y) \end{align*} \]

Regress \(X\) on \(Z\), let \(\hat{X} = P_Z X\)
Regress \(y\) on \(\hat{X}\)

IV Best Practices

Report the first stage regression of \(X\) on \(Z\)
- Check for relevance
Report the reduced form regression of \(Y\) on \(Z\)
If relevance at all in doubt, use weak identification robust confidence intervals
- E.g. ivmodels.summary with test='lagrange multiplier'

Example: Returns to Education

From Angrist and Krueger (1991)

Code

import graphviz as gr

g = gr.Digraph()
g.edge('Education', 'Earnings', style = 'dashed')
g.edge('Ability', 'Education')
g.edge('Ability', 'Earnings')
g.edge('?', 'Education')
g

Example: Returns to Education

Code

g = gr.Digraph()
g.edge('Education', 'Earnings', style = 'dashed')
g.edge('Ability', 'Education')
g.edge('Ability', 'Earnings')
g.edge('Quarter of Birth', 'Education')
g

import pandas as pd

df = pd.read_csv('data/ak91.csv')
df.head()

	log_wage	years_of_schooling	year_of_birth	quarter_of_birth	state_of_birth
0	5.790019	12.0	30.0	1.0	45.0
1	5.952494	11.0	30.0	1.0	45.0
2	5.315949	12.0	30.0	1.0	45.0
3	5.595926	12.0	30.0	1.0	45.0
4	6.068915	12.0	30.0	1.0	37.0

Example: Returns to Education

We must assume that
1. Relevance: \(\cov(QOB, Education) \neq 0\)
2. Exogeneity: \(Earnings \perp QOB \mid Education\)

Example: Relevance

import matplotlib.pyplot as plt
group_data = (df
    .groupby(["year_of_birth", "quarter_of_birth"])
    [["log_wage", "years_of_schooling"]]
    .mean()
    .reset_index()
    .assign(time_of_birth = lambda d: d["year_of_birth"] + (d["quarter_of_birth"])/4))

plt.figure(figsize=(6,6))
plt.plot(group_data["time_of_birth"], group_data["years_of_schooling"], zorder=-1)
for q in range(1, 5):
    x = group_data.query(f"quarter_of_birth=={q}")["time_of_birth"]
    y = group_data.query(f"quarter_of_birth=={q}")["years_of_schooling"]
    plt.scatter(x, y, marker="s", s=200, c=f"C{q}")
    plt.scatter(x, y, marker=f"${q}$", s=100, c=f"white")

plt.title("Years of Education by Quarter of Birth (first stage)")
plt.xlabel("Quarter of Birth")
plt.ylabel("Years of Schooling");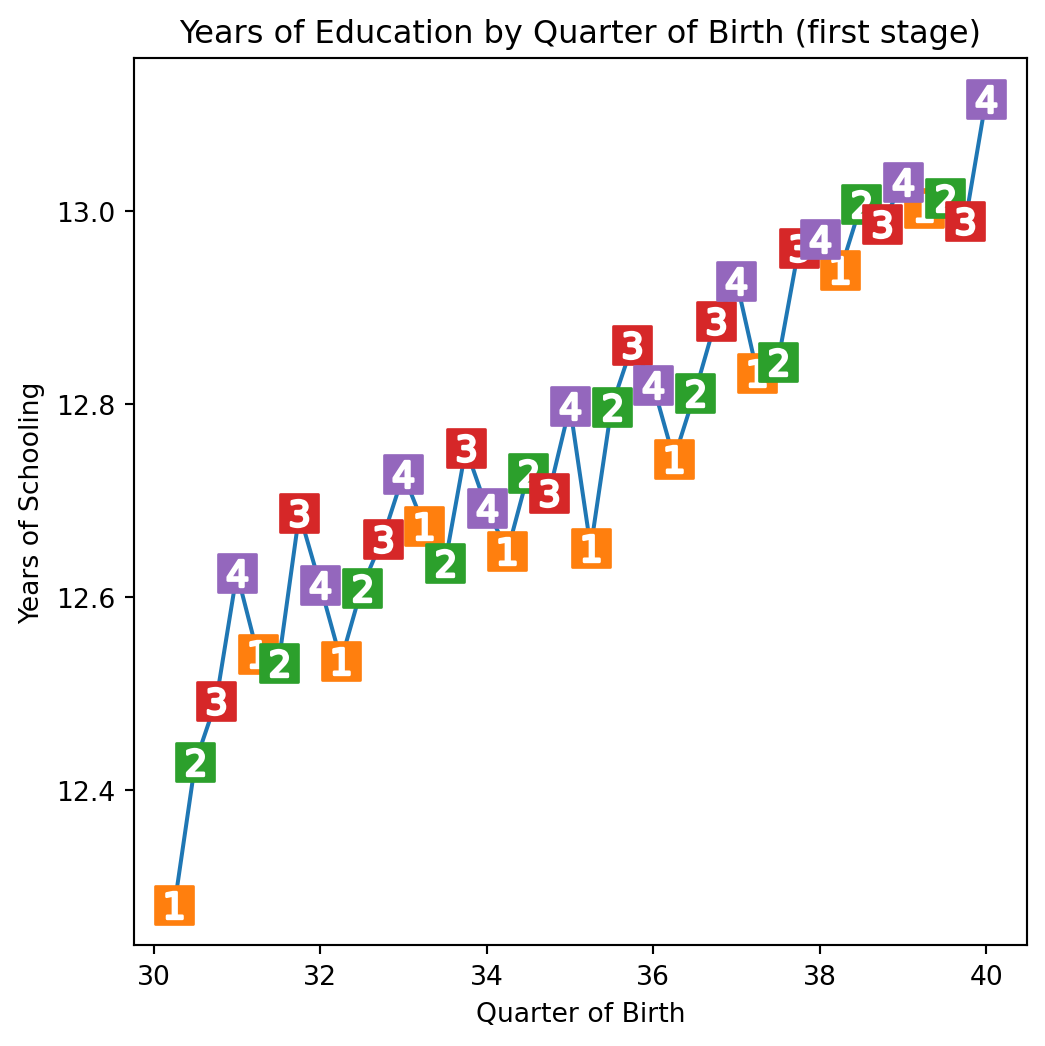

Example: Relevance

# Convert the quarter of birth to dummy variables
factor_data = df.assign(**{f"q{int(q)}": (df["quarter_of_birth"] == q).astype(int)
                             for q in df["quarter_of_birth"].unique()})

# Run the first stage regression
import statsmodels.formula.api as smf

first_stage = smf.ols("years_of_schooling ~ C(year_of_birth) + C(state_of_birth) + q4", data=factor_data).fit()

print("q4 parameter estimate:, ", first_stage.params["q4"])
print("q4 p-value:, ", first_stage.pvalues["q4"])

q4 parameter estimate:,  0.10085809272786722
q4 p-value:,  5.4648294166122615e-15

Example: Exogeneity

No way to test the exogeneity assumption
- Seems okay here
- Hard to come up with other reason why quarter of birth would affect earnings

Example: Reduced Form

# Plot the reduced form
plt.figure(figsize=(6,6))
plt.plot(group_data["time_of_birth"], group_data["log_wage"], zorder=-1)
for q in range(1, 5):
    x = group_data.query(f"quarter_of_birth=={q}")["time_of_birth"]
    y = group_data.query(f"quarter_of_birth=={q}")["log_wage"]
    plt.scatter(x, y, marker="s", s=200, c=f"C{q}")
    plt.scatter(x, y, marker=f"${q}$", s=100, c=f"white")

plt.title("Average Weekly Wage by Quarter of Birth (reduced form)")
plt.xlabel("Year of Birth")
plt.ylabel("Log Weekly Earnings");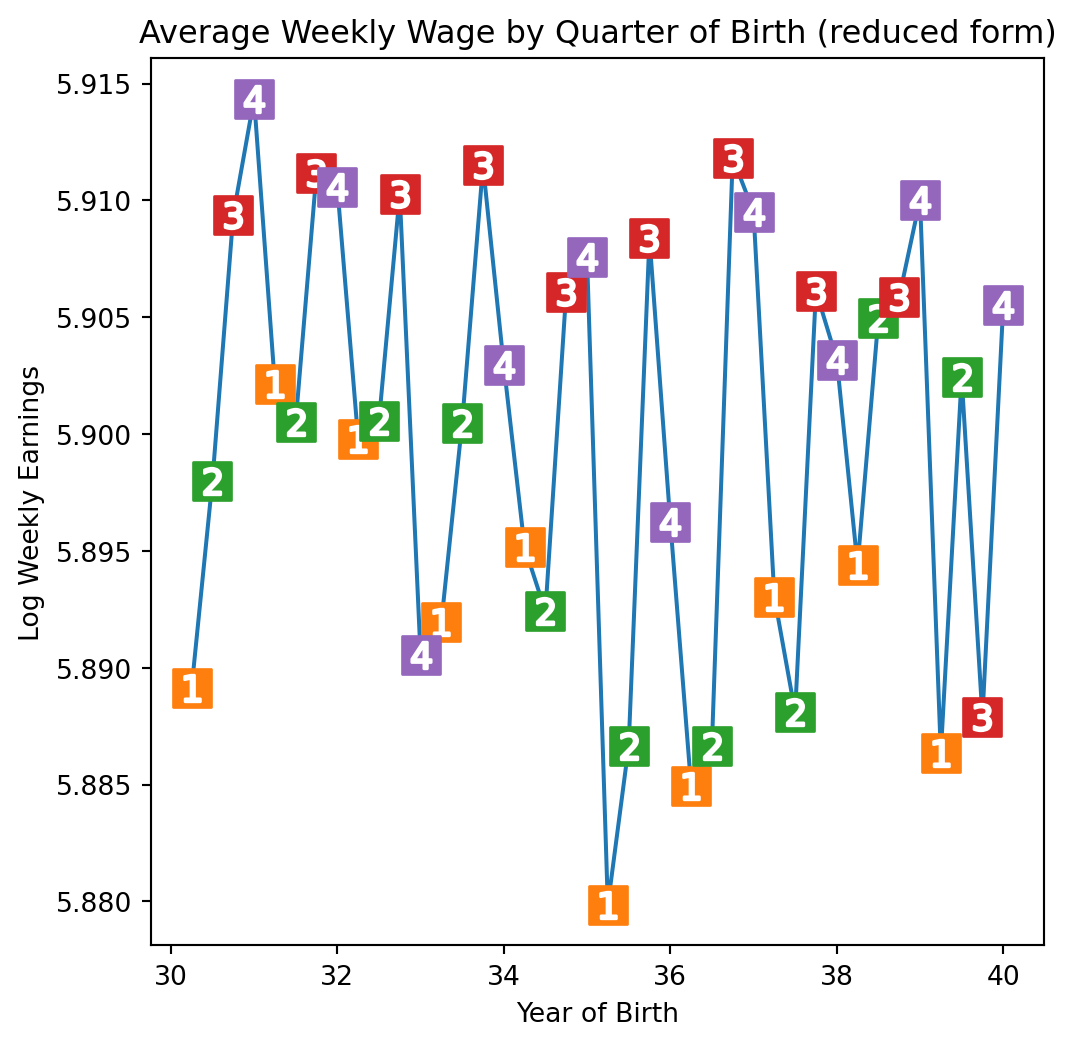

Example: Reduced Form

# Run the reduced form
reduced_form = smf.ols("log_wage ~ C(year_of_birth) + C(state_of_birth) + q4", data=factor_data).fit()

print("q4 parameter estimate:, ", reduced_form.params["q4"])
print("q4 p-value:, ", reduced_form.pvalues["q4"])

q4 parameter estimate:,  0.008603484260139821
q4 p-value:,  0.001494912718366322

Example: 2SLS

ate_iv = reduced_form.params["q4"] / first_stage.params["q4"]
print("ATE (IV):", ate_iv)

ATE (IV): 0.08530286492085

Example: Returns to Education

Use a package for IV
- ivmodels (best support for weak instrument robust inference)
- pyfixest.feols
- statsmodels.sandbox.regression.gmm.IV2SLS
- linearmodels.iv.IV2SLS

Example: `linearmodels`

from linearmodels.iv import IV2SLS

formula = 'log_wage ~ 1 + C(year_of_birth) + C(state_of_birth) + [years_of_schooling ~ q4]'
iv = IV2SLS.from_formula(formula, data=factor_data).fit()
print(iv.summary)

                          IV-2SLS Estimation Summary                          
==============================================================================
Dep. Variable:               log_wage   R-squared:                      0.1217
Estimator:                    IV-2SLS   Adj. R-squared:                 0.1215
No. Observations:              329509   F-statistic:                 1.028e+04
Date:                Mon, Nov 25 2024   P-value (F-stat)                0.0000
Time:                        10:41:48   Distribution:                 chi2(60)
Cov. Estimator:                robust                                         
                                                                              
                                     Parameter Estimates                                     
=============================================================================================
                           Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
---------------------------------------------------------------------------------------------
Intercept                     4.7468     0.2904     16.348     0.0000      4.1777      5.3158
C(year_of_birth)[T.31.0]     -0.0078     0.0063    -1.2384     0.2156     -0.0201      0.0045
C(year_of_birth)[T.32.0]     -0.0145     0.0073    -1.9698     0.0489     -0.0288   -7.25e-05
C(year_of_birth)[T.33.0]     -0.0174     0.0086    -2.0367     0.0417     -0.0342     -0.0007
C(year_of_birth)[T.34.0]     -0.0217     0.0094    -2.3012     0.0214     -0.0401     -0.0032
C(year_of_birth)[T.35.0]     -0.0344     0.0108    -3.1821     0.0015     -0.0556     -0.0132
C(year_of_birth)[T.36.0]     -0.0347     0.0118    -2.9309     0.0034     -0.0579     -0.0115
C(year_of_birth)[T.37.0]     -0.0410     0.0132    -3.0976     0.0020     -0.0670     -0.0151
C(year_of_birth)[T.38.0]     -0.0433     0.0152    -2.8520     0.0043     -0.0730     -0.0135
C(year_of_birth)[T.39.0]     -0.0547     0.0161    -3.3887     0.0007     -0.0864     -0.0231
C(state_of_birth)[T.2.0]      0.2272     0.1060     2.1433     0.0321      0.0194      0.4350
C(state_of_birth)[T.4.0]      0.1215     0.0404     3.0083     0.0026      0.0424      0.2007
C(state_of_birth)[T.5.0]      0.0431     0.0123     3.5103     0.0004      0.0190      0.0671
C(state_of_birth)[T.6.0]      0.1351     0.0557     2.4268     0.0152      0.0260      0.2442
C(state_of_birth)[T.8.0]      0.0920     0.0435     2.1143     0.0345      0.0067      0.1774
C(state_of_birth)[T.9.0]      0.1051     0.0429     2.4511     0.0142      0.0211      0.1891
C(state_of_birth)[T.10.0]     0.0796     0.0280     2.8408     0.0045      0.0247      0.1346
C(state_of_birth)[T.11.0]     0.1162     0.0572     2.0317     0.0422      0.0041      0.2282
C(state_of_birth)[T.12.0]    -0.0157     0.0278    -0.5651     0.5720     -0.0701      0.0387
C(state_of_birth)[T.13.0]    -0.0155     0.0119    -1.3003     0.1935     -0.0389      0.0079
C(state_of_birth)[T.15.0]     0.1256     0.0575     2.1857     0.0288      0.0130      0.2382
C(state_of_birth)[T.16.0]     0.0718     0.0497     1.4450     0.1485     -0.0256      0.1693
C(state_of_birth)[T.17.0]     0.1762     0.0429     4.1080     0.0000      0.0921      0.2603
C(state_of_birth)[T.18.0]     0.1341     0.0288     4.6494     0.0000      0.0775      0.1906
C(state_of_birth)[T.19.0]     0.0735     0.0382     1.9251     0.0542     -0.0013      0.1483
C(state_of_birth)[T.20.0]     0.0420     0.0462     0.9081     0.3638     -0.0486      0.1326
C(state_of_birth)[T.21.0]     0.1194     0.0153     7.7839     0.0000      0.0893      0.1495
C(state_of_birth)[T.22.0]     0.0883     0.0150     5.8957     0.0000      0.0589      0.1176
C(state_of_birth)[T.23.0]    -0.0236     0.0219    -1.0779     0.2811     -0.0666      0.0193
C(state_of_birth)[T.24.0]     0.1048     0.0225     4.6641     0.0000      0.0608      0.1489
C(state_of_birth)[T.25.0]     0.0783     0.0463     1.6916     0.0907     -0.0124      0.1691
C(state_of_birth)[T.26.0]     0.2035     0.0342     5.9550     0.0000      0.1365      0.2705
C(state_of_birth)[T.27.0]     0.1236     0.0393     3.1445     0.0017      0.0466      0.2006
C(state_of_birth)[T.28.0]    -0.0170     0.0133    -1.2800     0.2005     -0.0431      0.0090
C(state_of_birth)[T.29.0]     0.0955     0.0273     3.4927     0.0005      0.0419      0.1491
C(state_of_birth)[T.30.0]     0.0479     0.0469     1.0222     0.3067     -0.0440      0.1398
C(state_of_birth)[T.31.0]     0.0610     0.0442     1.3793     0.1678     -0.0257      0.1476
C(state_of_birth)[T.32.0]     0.1220     0.0609     2.0047     0.0450      0.0027      0.2413
C(state_of_birth)[T.33.0]     0.0036     0.0294     0.1226     0.9024     -0.0540      0.0611
C(state_of_birth)[T.34.0]     0.1390     0.0453     3.0702     0.0021      0.0503      0.2277
C(state_of_birth)[T.35.0]     0.0552     0.0285     1.9373     0.0527     -0.0006      0.1110
C(state_of_birth)[T.36.0]     0.1254     0.0517     2.4242     0.0153      0.0240      0.2268
C(state_of_birth)[T.37.0]    -0.0562     0.0100    -5.6174     0.0000     -0.0758     -0.0366
C(state_of_birth)[T.38.0]     0.1076     0.0360     2.9885     0.0028      0.0370      0.1781
C(state_of_birth)[T.39.0]     0.1429     0.0328     4.3559     0.0000      0.0786      0.2071
C(state_of_birth)[T.40.0]     0.0679     0.0349     1.9475     0.0515     -0.0004      0.1362
C(state_of_birth)[T.41.0]     0.1069     0.0515     2.0749     0.0380      0.0059      0.2079
C(state_of_birth)[T.42.0]     0.1103     0.0304     3.6256     0.0003      0.0507      0.1699
C(state_of_birth)[T.44.0]     0.0236     0.0352     0.6715     0.5019     -0.0454      0.0927
C(state_of_birth)[T.45.0]    -0.0723     0.0163    -4.4362     0.0000     -0.1043     -0.0404
C(state_of_birth)[T.46.0]     0.0500     0.0419     1.1946     0.2323     -0.0320      0.1321
C(state_of_birth)[T.47.0]     0.0513     0.0115     4.4653     0.0000      0.0288      0.0738
C(state_of_birth)[T.48.0]     0.0708     0.0262     2.7014     0.0069      0.0194      0.1221
C(state_of_birth)[T.49.0]     0.1001     0.0590     1.6968     0.0897     -0.0155      0.2158
C(state_of_birth)[T.50.0]    -0.0508     0.0276    -1.8360     0.0664     -0.1049      0.0034
C(state_of_birth)[T.51.0]     0.0362     0.0126     2.8697     0.0041      0.0115      0.0610
C(state_of_birth)[T.53.0]     0.1533     0.0511     2.9998     0.0027      0.0532      0.2535
C(state_of_birth)[T.54.0]     0.1256     0.0112     11.224     0.0000      0.1037      0.1476
C(state_of_birth)[T.55.0]     0.1051     0.0337     3.1212     0.0018      0.0391      0.1711
C(state_of_birth)[T.56.0]     0.1100     0.0548     2.0086     0.0446      0.0027      0.2174
years_of_schooling            0.0853     0.0255     3.3399     0.0008      0.0352      0.1354
=============================================================================================

Endogenous: years_of_schooling
Instruments: q4
Robust Covariance (Heteroskedastic)
Debiased: False

Example: `pyfixest`

import pyfixest as pf
ivpf = pf.feols('log_wage ~ 1 | state_of_birth + year_of_birth | years_of_schooling ~ q4', data=factor_data, vcov="HC1")
pf.etable(ivpf, type='md')

index                    est1
------------------  ---------
depvar               log_wage
-----------------------------
years_of_schooling  0.085***
                      (0.026)
-----------------------------
year_of_birth               x
state_of_birth              x
-----------------------------
Observations           329509
S.E. type              hetero
R2                          -
-----------------------------

Example: `ivmodels`

from patsy import dmatrices
import ivmodels
y,X = dmatrices("log_wage ~ 0 + years_of_schooling", data=factor_data, return_type='dataframe')
Z,controls = dmatrices("q4 ~  C(year_of_birth) + C(state_of_birth)", data=factor_data, return_type='dataframe')
controls.drop("Intercept", axis=1,inplace=True)

ivm = ivmodels.KClass(1).fit(X=X,y=y,Z=Z,C=controls)
sw = ivm.summary(X=X,y=y,Z=Z,C=controls, test='wald', feature_names=["years_of_schooling"])
print(sw)

Summary based on the wald test.

                    estimate  statistic    p-value          conf. set
years_of_schooling    0.0853      11.15  0.0008402  [0.03523, 0.1354]

Endogenous model statistic: 11.15, p-value: 0.0008402
(Multivariate) F-statistic: 61.09, p-value: 5.44e-15

Weak Instruments

One endogenous regressor, one instrument
- Structural equation \[ y_i = \beta_0 + \beta_1 x_i + \epsilon_i \]
- First stage \[ x_i = \pi_0^x + \pi_1^x z_i + u_i^x \]
- Reduced Form \[ y_i = \pi_0^y + \pi_1^y z_i + u_i^y \]
\(\text{2SLS} = \frac{\text{Reduced Form}}{\text{First Stage}}\)
\(\hat{\beta}^{2SLS}_1 = \frac{\hat{\pi}_1^y}{\hat{\pi}_1^x}\)

Weak Instruments

\(\hat{\beta}^{2SLS}_1 = \frac{\hat{\pi}_1^y}{\hat{\pi}_1^x}\)
If \(z\) not relevant, then divide by \(0\)
Even if \(z\) relevant, if \(\hat{\pi}_1^x\) is too likely near 0, then \(\hat{\beta}^{2SLS}_1\) will be messed up
- usual asymptotic normal distribution becomes a poor approximation to true finite sample distribution of \(\hat{\beta}^{2SLS}_1\)
“too likely near 0” is more common than one might think

Weak Instrument Simulation

First stage \(X = Z\gamma + e\), simulation with \(\Er[Z_i Z_i] = I\) and \(e \sim N(0,0.25)\), so first stage \(t \approx \sqrt{n}\gamma/0.5\)
Distribution of \(\hat{\beta}^{2SLS}\) with \(\gamma = 1\), \(\gamma=0.5\), \(\gamma=0.2\), and \(\gamma=0.1\) and \(n=100\)
- implies first stage t-statistics of \(20\), \(10\), \(4\), and \(2\)

Weak Instrument Simulation : \(\hat{\beta}^{2SLS}\)

import seaborn as sns
import numpy as np
import scipy
n = 100
gamma = [1,0.5, 0.2,0.1]
sig = 0.5
Exe=1.0

def simiv(n,gamma,sig, b0, Exe):
   z = np.random.randn(n)
   xe = np.random.randn(n)
   x = z*gamma + (xe*Exe + np.random.randn(n))/np.sqrt(1+Exe**2)*sig
   e = xe + np.random.randn(n)
   y = x*b0 + e
   return(y,x,z)

def b2sls(y,x,z) :
    return(np.dot(z,y)/np.dot(z,x))

S = 10_000
fig, ax = plt.subplots(2,2)
x = np.linspace(-3,3,num=300)
b0 = 1

for j in range(len(gamma)):
    se = np.sqrt(2/n)/(gamma[j])
    phix = scipy.stats.norm(loc=b0,scale=se).pdf(x*se + b0)
    b = np.array([(lambda x: b2sls(x[0],x[1],x[2]))(simiv(n,gamma[j],sig,b0,Exe)) for _ in range(S)])
    sns.histplot(b, ax=ax.flat[j], stat='density')
    ax.flat[j].set_title(f"First stage E[t]={np.sqrt(n)*gamma[j]/sig:.3}")
    ax.flat[j].plot(x*se+b0,phix)
    ax.flat[j].set_xlim(-3*se +1,3*se+1)

Weak Instrument Simulation : \(\hat{\beta}^{2SLS}\)

Weak Instrument Simulation : t-stat

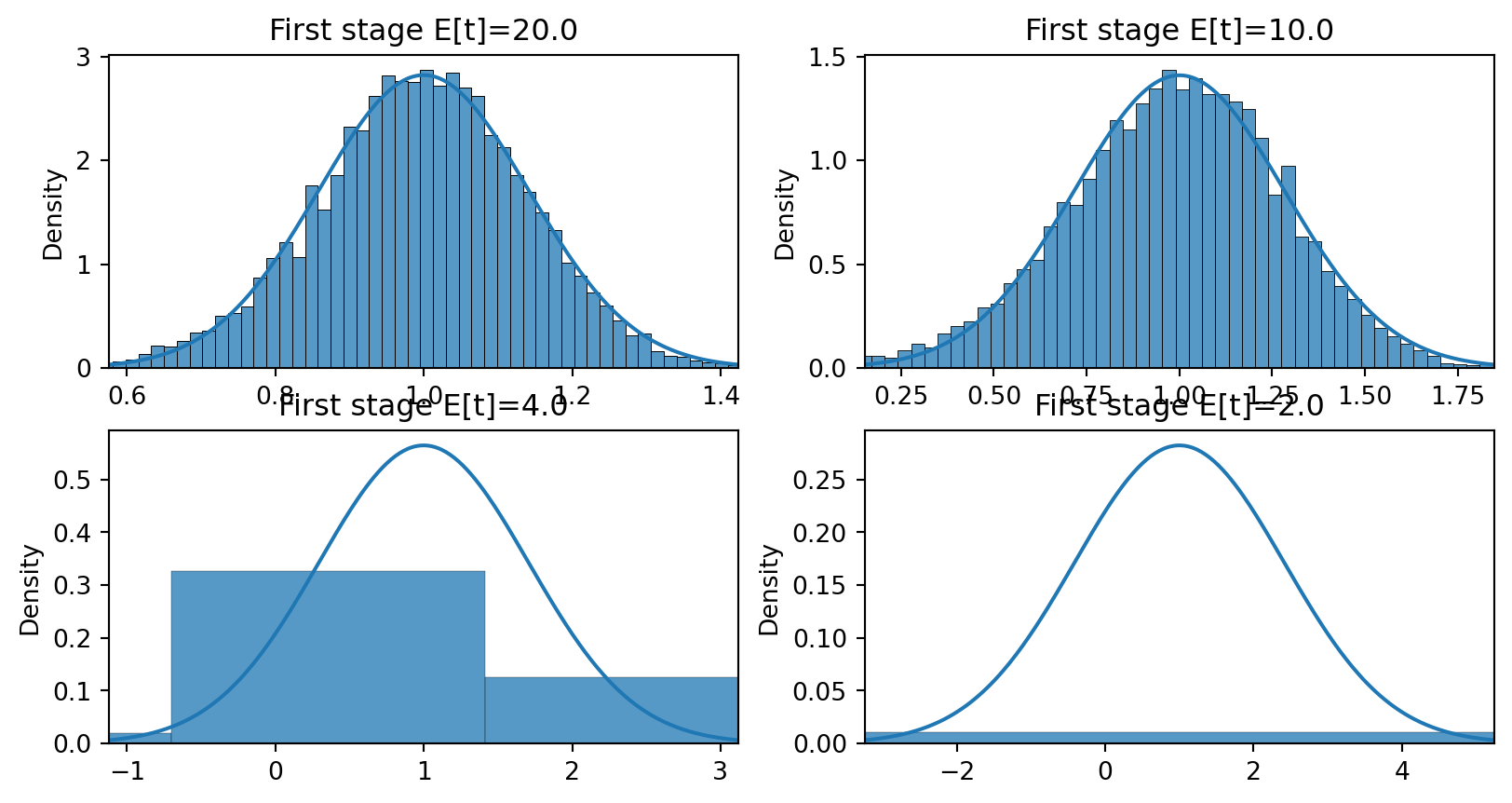
def t2sls(y,x,z, b0=1) :
    b = b2sls(y,x,z)
    u = y - x*b
    se = np.sqrt(u.var()*np.dot(z,z)/(np.dot(x,z)**2))
    t = (b-b0)/se
    return(t)

S = 10_000
fig, ax = plt.subplots(2,2)
x = np.linspace(-3,3,num=300)
phix = scipy.stats.norm.pdf(x)
for j in range(len(gamma)):
    ts = np.array([(lambda x: t2sls(x[0],x[1],x[2],b0=b0))(simiv(n,gamma[j],sig,b0,Exe)) for _ in range(S)])
    sns.histplot(ts, ax=ax.flat[j], stat='density')
    ax.flat[j].set_title(f"First stage E[t]={np.sqrt(n)*gamma[j]/sig:.3}")
    ax.flat[j].plot(x,phix)
    ax.flat[j].set_xlim(-3,3)

Weak Instrument Simulation : t-stat

Weak Instruments

Lessons from simulation:
- When \(\Er[Z_i X_i']\) is small, usual asymptotic distribution is a poor approximation for the finite sample distribution of \(\hat{\beta}^{IV}\)
- The approximation can be poor even when \(H_0: \gamma = 0\) in \(X = Z\gamma + e\) would be rejected

First stage F-statistic

Always report first stage “effective” F-statistic

y,x,z = simiv(n,gamma[3],sig, b0, Exe)
model=pf.feols('y ~ 1 | 0 | x ~ z', pd.DataFrame({'y':y,'x':x, 'z': z}))
model.IV_Diag()
model._eff_F

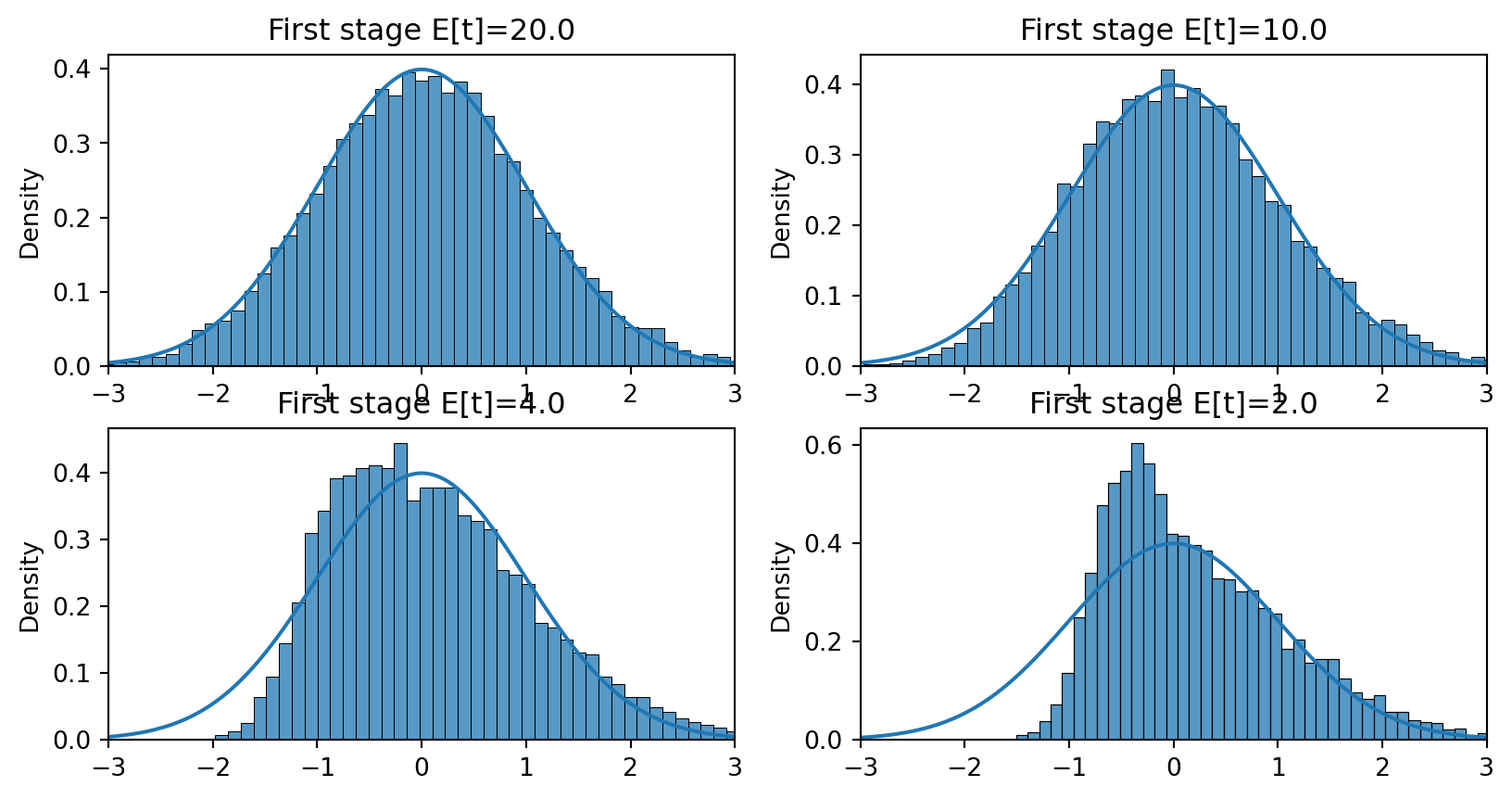
np.float64(6.183024655354665)

If \(F >> 100\), everything okay
- (old advice of \(F>10\) is not enough)
- Even larger needed if more instruments
Else, use different method for confidence intervals and testing

Identification Robust Inference

Can we find a better approximation to the finite sample distribution when \(\Er[Z_i X_i']\) is small?
Yes, two approaches lead to the same answers:
1. Require uniform (over values of \(\Er[Z_iX_i']\)) converge
2. Weak instrument asymptotics (instead of \(\Er[Z_i X_i]\) fixed with \(n\), suppose \(\Er[Z_i X_i'] = C/\sqrt{n}\))
Identification robust tests:
- Anderson Rubin (okay when just identified — number of instruments = number of endogenous regressors)
- Conditional likelihood ratio
- Lagrange multiplier

Identification Robust Inference

ivmodels from Londschien and Bühlmann (2024) seems like best python package
- convenient confidence intervals
- downside: assumes homoscedasticity

y,X = dmatrices("log_wage ~ 0 + years_of_schooling", data=factor_data, return_type='dataframe')
Z,controls = dmatrices("q4 ~  C(year_of_birth) + C(state_of_birth)", data=factor_data, return_type='dataframe')
controls.drop("Intercept", axis=1,inplace=True)
ivm = ivmodels.KClass(1).fit(X=X,y=y,Z=Z,C=controls)
sa = ivm.summary(X=X,y=y,Z=Z,C=controls, test='anderson-rubin', feature_names=["years_of_schooling"])
print(sa)

Summary based on the anderson-rubin test.

                    estimate  statistic   p-value          conf. set
years_of_schooling    0.0853      10.09  0.001495  [0.03477, 0.1382]

Endogenous model statistic: 10.09, p-value: 0.001495
(Multivariate) F-statistic: 61.09, p-value: 5.44e-15

Identification Robust Inference

sl = ivm.summary(X=X,y=y,Z=Z,C=controls, test='lagrange multiplier', feature_names=["years_of_schooling"])
print(sl)

Summary based on the lagrange multiplier test.

                    estimate  statistic   p-value          conf. set
years_of_schooling    0.0853      10.09  0.001495  [0.03477, 0.1382]

Endogenous model statistic: 10.09, p-value: 0.001495
(Multivariate) F-statistic: 61.09, p-value: 5.44e-15

Sources and Further Reading

Chapter 8 and 9 of Facure (2022)
Chapters 6, 12, and 13 of Chernozhukov et al. (2024)
The Effect: Chapter 19 - Instrumental Variables Huntington-Klein (2021)

References

Angrist, Joshua D., and Alan B. Krueger. 1991. “Does Compulsory School Attendance Affect Schooling and Earnings?” The Quarterly Journal of Economics 106 (4): pp. 979–1014. http://www.jstor.org/stable/2937954.

Chernozhukov, V., C. Hansen, N. Kallus, M. Spindler, and V. Syrgkanis. 2024. Applied Causal Inference Powered by ML and AI. https://causalml-book.org/.

Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.

Huntington-Klein, Nick. 2021. The Effect: An Introduction to Research Design and Causality. CRC Press. https://theeffectbook.net/.

Londschien, Malte, and Peter Bühlmann. 2024. “Weak-Instrument-Robust Subvector Inference in Instrumental Variables Regression: A Subvector Lagrange Multiplier Test and Properties of Subvector Anderson-Rubin Confidence Sets.” https://arxiv.org/abs/2407.15256.

Instrumental Variables

Introduction

Endogeneity

Sources of Endogeneity

Omitted Variables

Omitted Variables Bias

Simultaneity

Simultaneity

Measurment Error

Instrumental Variables

Instrumental Variables

Instrumental Variables Estimator

Two Stage Least Squares

IV Best Practices

Example: Returns to Education

Example: Returns to Education

Example: Returns to Education

Example: Returns to Education

Example: Relevance

Example: Relevance

Example: Exogeneity

Example: Reduced Form

Example: Reduced Form

Example: 2SLS

Example: Returns to Education

Example: linearmodels

Example: pyfixest

Example: ivmodels

Weak Instruments

Weak Instruments

Weak Instruments

Weak Instrument Simulation

Weak Instrument Simulation : \(\hat{\beta}^{2SLS}\)

Weak Instrument Simulation : \(\hat{\beta}^{2SLS}\)

Weak Instrument Simulation : t-stat

Weak Instrument Simulation : t-stat

Weak Instruments

First stage F-statistic

Identification Robust Inference

Identification Robust Inference

Identification Robust Inference

Sources and Further Reading

References

Example: `linearmodels`

Example: `pyfixest`

Example: `ivmodels`