Matching

ECON526

Paul Schrimpf

University of British Columbia

Introduction

Setting

  • Potential outcomes \((Y(0), Y(1))\)
  • Treatment \(T \in \{0,1\}\)
  • Observe \(Y = Y(T)\)
  • Covariates \(X\)
  • Assume conditional independence \((Y(0),Y(1)) \perp T | X\)

\[ \def\Er{{\mathrm{E}}} \def\En{{\mathbb{En}}} \def\cov{{\mathrm{Cov}}} \def\var{{\mathrm{Var}}} \def\R{{\mathbb{R}}} \newcommand\norm[1]{\left\lVert#1\right\rVert} \def\rank{{\mathrm{rank}}} \newcommand{\inpr}{ \overset{p^*_{\scriptscriptstyle n}}{\longrightarrow}} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \DeclareMathOperator*{\argmin}{argmin} \]

Why not regression?

  • Average treatment effect \[ ATE = \int \Er[Y|T=1,X=x] - \Er[Y|T=0,X=x] dP(x) \]
  • Regression gives the best linear approximation to \(\Er[Y|T,X]\), so why not just estimate linear regression \[ Y_i = \hat{\alpha} T_i + X_i'\hat{\beta} + \hat{\epsilon}_i \] and, and then use \(\hat{\alpha}\) as an estimate of the ATE?

Why not regression?

  • Partial out (Frish-Waugh-Lovell theorem) \[ \begin{align*} \hat{\alpha} = & \frac{\frac{1}{n} \sum_{i=1}^n Y_i (T_i - X_i'(X'X)^{-1}X'T)} {\frac{1}{n} \sum_{i=1}^n (T_i - X_i'(X'X)^{-1}X'T)^2} \\ \inprob & \Er\left[Y_i \underbrace{\frac{T_i - X_i'\pi}{\Er[(T_i - X_i'\pi)^2]}}_{\equiv \omega(T_i,X_i)}\right] \\ = & \Er\left[Y_{0,i} \omega(T_i,X_i)\right] + \Er\left[(Y_{1,i}-Y_{0,i}) \omega(T_i,X_i)T_i\right] \end{align*} \] where \(\pi = \argmin_{\tilde{\pi}} \Er[(T_i - X_i'\tilde{\pi})^2]\)

  • Note: \(\Er[\omega(T,X)] = 0\), \(\Er[T\omega(T,X)] = 1\)

Why not regression?

  • \(\plim \hat{\alpha} = \Er\left[Y_{0,i} \omega(T_i,X_i)\right] + \Er\left[(Y_{1,i}-Y_{0,i}) \omega(T_i,X_i)T_i\right]\)

  • What can be in the range of \(\omega(T,X) = \frac{T - X'\pi}{\Er[(T_i - X_i'\pi)^2]}\)?

Why not regression?

imports 
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import scipy
style.use("fivethirtyeight")
np.random.seed(1234)

def simulate(n, pi=np.array([0,1])):
    X = np.random.randn(n, len(pi))
    X[:,0] = 1
    P = np.clip(scipy.stats.norm.cdf(X @ pi), 0.05, 0.95)
    T = 1*(np.random.rand(n) < P)
    Ey0x = np.zeros(n)
    Ey1x = np.exp(3*(X[:,1]-2))
    y0 = Ey0x + np.random.randn(n)
    y1 = Ey1x + np.random.randn(n)
    y = T*y1 + (1-T)*y0
    return(X,T,y,y0,y1, Ey0x, Ey1x, P)

X,T,y,y0,y1,Ey0x,Ey1x,P = simulate(4000)

pihat = np.linalg.solve(X.T @ X, X.T @ T)
w = T - X @ pihat
w = w/np.mean(w**2);

Why not regression?

TX = np.hstack((T.reshape(len(T),1),X))
abhat = np.linalg.solve(TX.T @ TX, TX.T @ y)
ahat = abhat[0]
print(ahat)
-0.11952795827329041
np.mean(y1-y0)
np.float64(0.1172689998868494)
  • Weights, \(\omega(T,X)\), are not all positive, so the regression estimate can be negative even if \(\Er[Y(1) | X] - \Er[Y(0)|X]\) is positive everywhere

Why not regression?

plot 
import matplotlib.cm as cm
fig, axes = plt.subplots(2, 1, figsize=(6, 6))

# Create a scatter plot for the first panel (left)
axes[0].scatter(X[:,1], w, c=T, cmap=cm.Dark2)
axes[0].set_xlabel("X")
axes[0].set_ylabel("ωT")
axes[0].set_title("Weights")

axes[1].scatter(X[:,1], y1-y0, label="TE")
axes[1].set_xlabel("X")
axes[1].set_ylabel("Y₁ - Y₀")
axes[1].set_title("Treatment effects")
sort_idx = np.argsort(X[:,1])
axes[1].plot(X[sort_idx,1], Ey1x[sort_idx]-Ey0x[sort_idx], label="E[y1-y0|x]")

# Display the plot
plt.tight_layout()  # Ensure proper layout spacing
plt.show()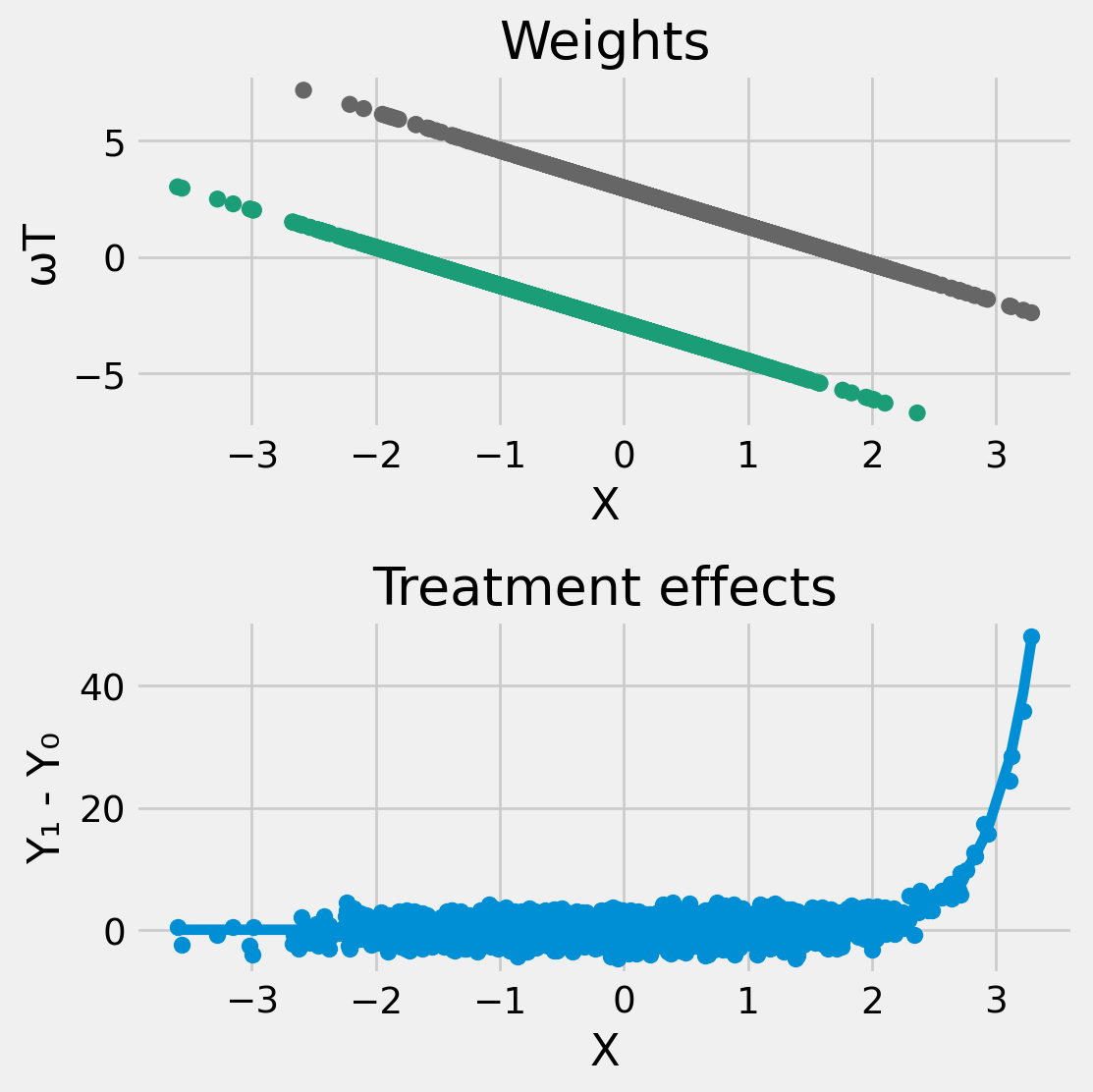

Matching

Matching

  • If not regression, then what? \[ ATE = \int \Er[Y|T=1,X=x] - \Er[Y|T=0,X=x] dP(x) \]

Plug-in estimator

  • Plug in estimator: \[ \widehat{ATE} = \frac{1}{n} \sum_{i=1}^n \left(\hat{E}[Y|T=1,X=X_i] - \hat{E}[Y|T=0,X=X_i] \right) \] where \(\hat{E}[Y|T,X]\) is some flexible estimator for \(\Er[Y|T,X]\)
    • if \(X\) is discrete, \(\hat{E}\) can be conditional averages or equivalently, “saturated” regression
    • if \(X\) continuous, \(\hat{E}\) can be some nonparametric regression estimator
    • Original approaches to this problem used nearest neighbor matching to estimate \(\hat{E}[Y|T,X]\)
  • Downside:
    • Difficult statistical properties — choice of tuning parameters, strong assumptions needed, failure of bootstrap for nearest neighbors Abadie and Imbens (2008)

Propensity Score

  • Let \(p(X) = P(T=1|X=X)\)
  • Note: \[ \begin{align*} \Er[Y|X,T=1] - \Er[Y|X,T=0] = & E\left[\frac{Y T}{p(X)}|X \right] - E\left[\frac{Y(1-T)}{1-p(X)}|X \right] \\ = & E\left[ Y \frac{T - p(X)}{p(X)(1-p(X))} | X \right] \end{align*} \]

Propensity Score

  • so \[ ATE = \Er\left[ \frac{Y T}{p(X)} - \frac{Y(1-T)}{1-p(X)}\right] = \Er\left[ Y \frac{T - p(X)}{p(X)(1-p(X))} \right] \]

Inverse propensity weighting

  • Estimator \[ \widehat{ATE}^{IPW} = \frac{1}{n} \sum_{i=1}^n \frac{Y_iT_i}{\hat{p}(X_i)} - \frac{Y_i(1-T_i)}{1-\hat{p}(X_i)} \] where \(\hat{p}(X)\) is some flexible estimator for \(P(T=1|X)\)

  • Downside:

    • Difficult statistical properties — choice of tuning parameters, strong assumptions needed

Doubly Robust Estimator

  • Combines plug-in and IPW estimators
  • Estimator \[ \begin{align*} \widehat{ATE}^{DR} = & \frac{1}{n} \sum_{i=1}^n \hat{E}[Y|T=1,X=X_i] - \hat{E}[Y|T=0,X=X_i] + \\ & + \frac{1}{n} \sum_{i=1}^n \frac{T_i(Y_i - \hat{E}[Y|T=1,X=X_i])}{\hat{p}(X_i)} - \\ & - \frac{(1-T_i)(Y_i - \hat{E}[Y|T=0,X=X_i])} {1-\hat{p}(X_i)} \end{align*} \]

Doubly Robust Estimator

  • Doubly robust in that:
    • Consistent as long as either \(\hat{p}(X) \inprob p(X)\) or \(\hat{E}[Y|T,X] \inprob \Er[Y|T,X]\)
    • Insensitive to small changes in \(\hat{p}(X)\) or \(\hat{E}[Y|T,X]\)
  • Allows nicer statistical properties
    • Weaker assumptions needed
    • Asymptotic distribution is the same as if \(p(X)\) and \(\Er[Y|T,X]\) were known

Software

  • Advice: use the doubly robust estimator with nonparametric estimates for \(\hat{E}[Y|T,X]\) and \(\hat{p}(X)\)
  • Recommended package:

Example: simulation

  • Infeasible estimator: average of \(Y(1) - Y(0)\)
se = np.sqrt(np.var(y1-y0)/len(y1))
ate = np.mean(y1-y0)
print(f"Infeasible estimator with potential outcomes observed = {ate:.2} with 95% CI = [{ate-1.96*se:.2},{ate+1.96*se:.2}]\n")
Infeasible estimator with potential outcomes observed = 0.12 with 95% CI = [0.058,0.18]
  • Infeasible estimator: doubly robust with true \(\Er[Y(T)|X]\) and \(p(X)\)
aipw = Ey1x - Ey0x + T*(y - Ey1x)/P - (1-T)*(y - Ey0x)/(1-P)
se = np.sqrt(np.var(aipw)/len(aipw))
print(f"Infeasible estimator with true E[y1-y0|x] = and p(x) {np.mean(aipw):.2} with 95% CI = [{np.mean(aipw)-1.96*se:.2},{np.mean(aipw)+1.96*se:.2}]\n")
Infeasible estimator with true E[y1-y0|x] = and p(x) 0.15 with 95% CI = [0.057,0.24]

Example: choosing flexible estimators

from sklearn.ensemble import GradientBoostingRegressor, GradientBoostingClassifier
from sklearn.linear_model import LassoCV, LogisticRegressionCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.kernel_approximation import RBFSampler
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline

gamma = 0.5
nc = 100
models = [
    Pipeline([('rbf',RBFSampler(gamma=gamma, random_state=1, n_components=nc)),
              ('lasso',LassoCV(max_iter=10_000, tol=1e-2, n_jobs=-1, selection='random',
                               alphas=10**np.linspace(-3,3,20)))]),
    Pipeline([('poly',PolynomialFeatures(degree=10)),
              ('scale', StandardScaler()),
              ('lasso',LassoCV(max_iter=10_000, n_jobs=-1, selection='random', tol=1e-2,
                               alphas=10**np.linspace(-3,3,20)))]),
    GradientBoostingRegressor(learning_rate=0.1, criterion="squared_error")]

for m in models :
    print(m)
    print(f"cross val R-squared {cross_val_score(m, X, y, cv=5).mean():.4} \n\n")
Pipeline(steps=[('rbf', RBFSampler(gamma=0.5, random_state=1)),
                ('lasso',
                 LassoCV(alphas=array([1.00000000e-03, 2.06913808e-03, 4.28133240e-03, 8.85866790e-03,
       1.83298071e-02, 3.79269019e-02, 7.84759970e-02, 1.62377674e-01,
       3.35981829e-01, 6.95192796e-01, 1.43844989e+00, 2.97635144e+00,
       6.15848211e+00, 1.27427499e+01, 2.63665090e+01, 5.45559478e+01,
       1.12883789e+02, 2.33572147e+02, 4.83293024e+02, 1.00000000e+03]),
                         max_iter=10000, n_jobs=-1, selection='random',
                         tol=0.01))])
cross val R-squared 0.4365 


Pipeline(steps=[('poly', PolynomialFeatures(degree=10)),
                ('scale', StandardScaler()),
                ('lasso',
                 LassoCV(alphas=array([1.00000000e-03, 2.06913808e-03, 4.28133240e-03, 8.85866790e-03,
       1.83298071e-02, 3.79269019e-02, 7.84759970e-02, 1.62377674e-01,
       3.35981829e-01, 6.95192796e-01, 1.43844989e+00, 2.97635144e+00,
       6.15848211e+00, 1.27427499e+01, 2.63665090e+01, 5.45559478e+01,
       1.12883789e+02, 2.33572147e+02, 4.83293024e+02, 1.00000000e+03]),
                         max_iter=10000, n_jobs=-1, selection='random',
                         tol=0.01))])
cross val R-squared 0.5392 


GradientBoostingRegressor(criterion='squared_error')
cross val R-squared 0.5006

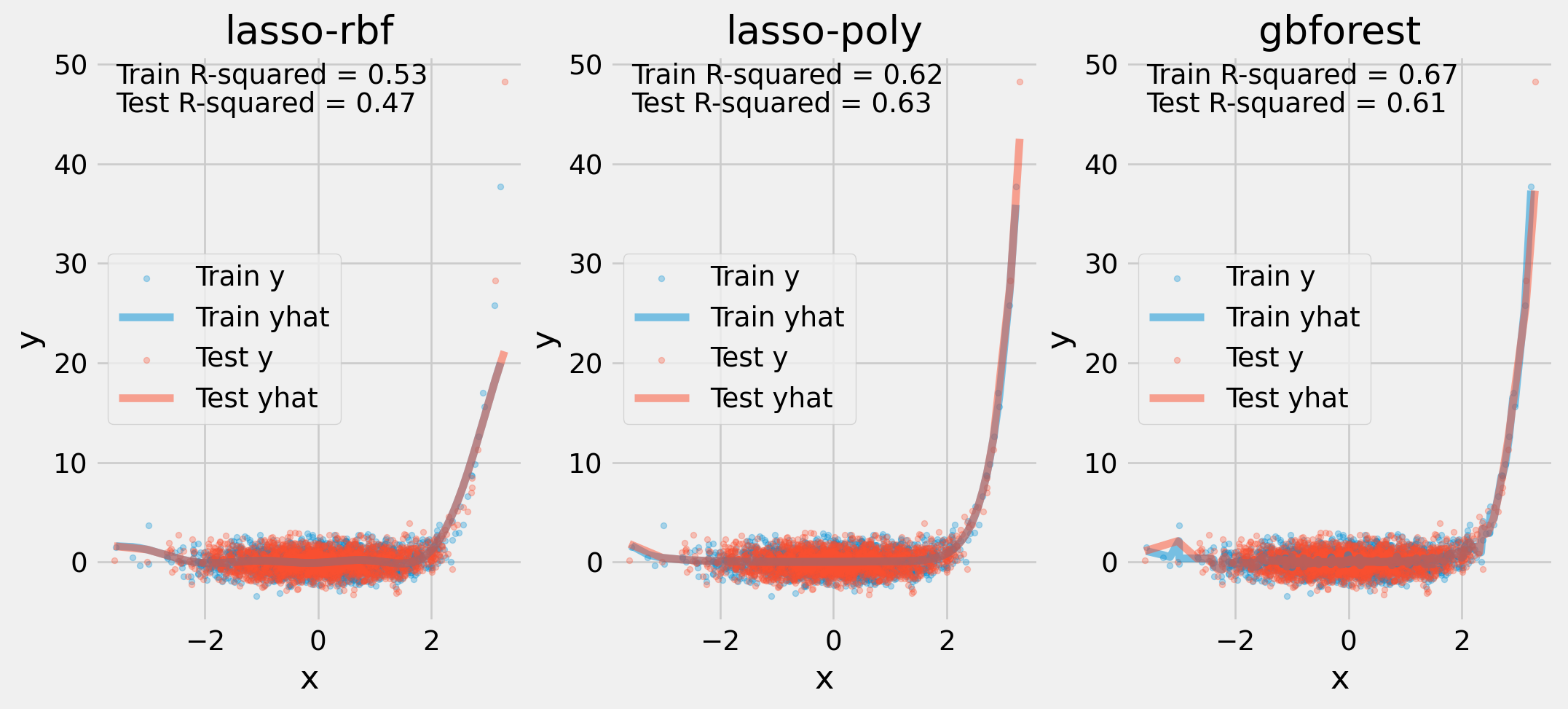
Visualizing Fit

from sklearn.model_selection import train_test_split
names = ["lasso-rbf", "lasso-poly", "gbforest"]
X_train,  X_test,y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=5498)
fig, ax = plt.subplots(1,3, figsize=(12,5))
ax = ax.flatten()
def r2(y,yhat) :
    return(1 - np.mean((y-yhat)**2)/np.var(y))
otr = np.argsort(X_train[:,1])
ote = np.argsort(X_test[:,1])

for i, m in enumerate(models):
    m.fit(X_train,y=y_train)
    yhat = m.predict(X_train)
    yhat_test = m.predict(X_test)
    ax[i].scatter(X_train[:,1], y_train, alpha=0.3, label="Train y", color="C0", marker=".")
    ax[i].plot(X_train[otr,1], yhat[otr], alpha=0.5, label="Train yhat", color="C0")
    ax[i].scatter(X_test[:,1], y_test, alpha=0.3, label="Test y", color="C1", marker=".")
    ax[i].plot(X_test[ote,1], yhat_test[ote], alpha=0.5, label="Test yhat", color="C1")
    ax[i].set_xlabel("x")
    ax[i].set_ylabel("y")
    ax[i].set_title(names[i])
    ax[i].annotate(f"Train R-squared = {r2(y_train, yhat):.2}", (0.05, 0.95), xycoords='axes fraction')
    ax[i].annotate(f"Test R-squared = {r2(y_test, yhat_test):.2}", (0.05, 0.90), xycoords='axes fraction')
    ax[i].legend()

plt.show()

Visualizing Fit

Example: choosing flexible estimators

gamma = 0.5
nc = 100
models = [
    Pipeline([('rbf',RBFSampler(gamma=gamma, random_state=1, n_components=nc)),
              ('logistic',LogisticRegressionCV(n_jobs=-1, scoring='neg_log_loss'))]),
    Pipeline([('poly',PolynomialFeatures(degree=10)),
              ('scale', StandardScaler()),
              ('logistic',LogisticRegressionCV(n_jobs=-1, scoring='neg_log_loss'))]),
    GradientBoostingClassifier(learning_rate=0.1)]
for m in models :
    print(m)
    print(f"cross val log likelihood {cross_val_score(m, X, T, scoring='neg_log_loss', cv=5).mean():.4} \n\n")
Pipeline(steps=[('rbf', RBFSampler(gamma=0.5, random_state=1)),
                ('logistic',
                 LogisticRegressionCV(n_jobs=-1, scoring='neg_log_loss'))])
cross val log likelihood -0.5077 


Pipeline(steps=[('poly', PolynomialFeatures(degree=10)),
                ('scale', StandardScaler()),
                ('logistic',
                 LogisticRegressionCV(n_jobs=-1, scoring='neg_log_loss'))])
cross val log likelihood -0.5098 


GradientBoostingClassifier()
cross val log likelihood -0.5184

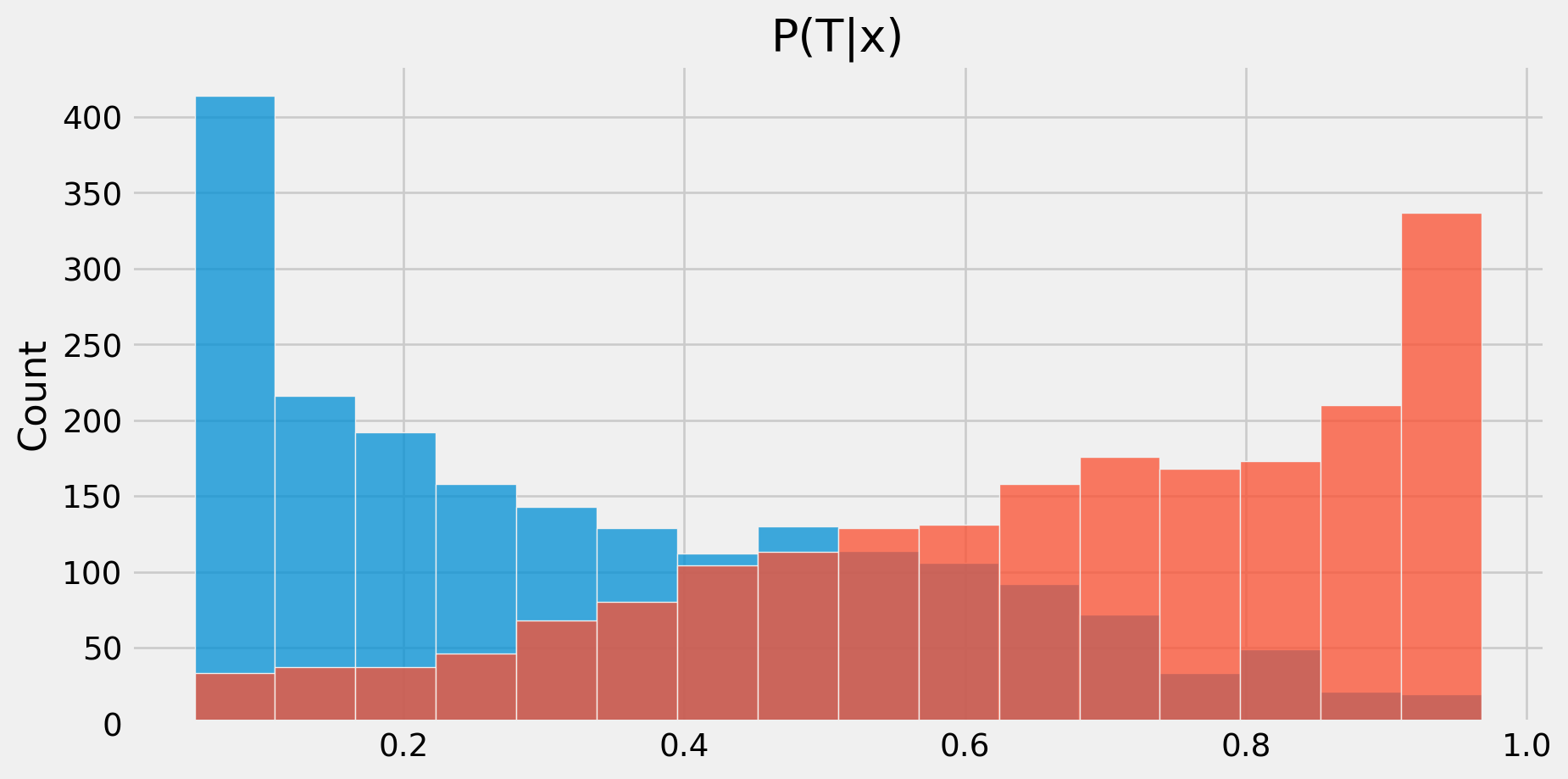
Example: Checking Overlap

import seaborn as sns
import matplotlib.pyplot as plt
import doubleml as dml
g = Pipeline([('poly',PolynomialFeatures(degree=10)),
              ('scale', StandardScaler()),
              ('lasso',LassoCV(max_iter=10_000, n_jobs=-1, selection='random', tol=1e-2,
                               alphas=10**np.linspace(-3,3,20)))])
m = Pipeline([('rbf',RBFSampler(gamma=gamma, random_state=1, n_components=nc)),
              ('logistic',LogisticRegressionCV(n_jobs=-1, scoring='neg_log_loss'))])

m.fit(X,T)

def plotp(model,X,d):
    fig,ax=plt.subplots()
    p = model.predict_proba(X)
    sns.histplot(p[d==0,1], kde = False,
                 label = "Untreated", ax=ax)
    sns.histplot(p[d==1,1], kde = False,
                 label = "Treated", ax=ax)
    ax.set_title('P(T|x)')
    return(fig)

fig=plotp(m, X, T)

Example: Checking Overlap

Example: Results

dmldata = dml.DoubleMLData.from_arrays(X, y, T)
dmlATE = dml.DoubleMLAPOS(dmldata, g, m, treatment_levels=[0, 1])
dmlATE.fit()
dmlATE.summary
coef std err t P>|t| 2.5 % 97.5 %
0 -0.021252 0.030485 -0.697120 0.485728 -0.081001 0.038497
1 0.131497 0.038623 3.404609 0.000663 0.055797 0.207197 
dmlATE.causal_contrast(0).summary
coef std err t P>|t| 2.5 % 97.5 %
1 vs 0 0.152749 0.049476 3.087356 0.002019 0.055778 0.249719 
aipw = Ey1x - Ey0x + T*(y - Ey1x)/P - (1-T)*(y - Ey0x)/(1-P)
se = np.sqrt(np.var(aipw)/len(aipw))
print(f"Infeasible estimator with true E[y1-y0|x] = and p(x) {np.mean(aipw):.2} with 95% CI = [{np.mean(aipw)-1.96*se:.2},{np.mean(aipw)+1.96*se:.2}]\n")
Infeasible estimator with true E[y1-y0|x] = and p(x) 0.15 with 95% CI = [0.057,0.24]

Growth Mindset

National Study of Learning Mindsets

  • Original study by Yeager et al. (2019)
  • Synthetic data created by Athey and Wager (2019), downloaded from Facure (2022)

Data

imports 
import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
style.use("fivethirtyeight")
pd.set_option("display.max_columns", 20)
datadir="./data"
data = pd.read_csv(datadir+"/learning_mindset.csv")
data.sample(5, random_state=431)
schoolid intervention achievement_score success_expect ethnicity gender frst_in_family school_urbanicity school_mindset school_achievement school_ethnic_minority school_poverty school_size
9366 9 0 1.137192 6 1 1 1 4 1.324323 -1.311438 1.930281 0.281143 0.362031
7810 27 0 -0.554268 5 2 1 1 1 0.240267 -0.785287 0.611807 0.612568 -0.116284
7532 29 0 -0.462576 6 1 1 1 1 -0.373087 0.113096 -0.833417 -1.924778 -1.147314
10381 1 0 -0.402644 5 2 2 1 3 1.185986 -1.129889 1.009875 1.005063 -1.174702
1244 57 1 1.528680 6 4 1 1 2 0.097162 -0.292353 -1.030865 -0.813799 0.184716

Evidence of Confounding

Code 
def std_error(x):
    return np.std(x, ddof=1) / np.sqrt(len(x))

grouped = data.groupby('success_expect')['intervention'].agg(['mean', std_error])
grouped = grouped.reset_index()

fig, ax = plt.subplots()
plt.errorbar(grouped['success_expect'],grouped['mean'],yerr=1.96*grouped['std_error'],fmt="o")
ax.set_xlabel('student expectation of success')
ax.set_ylabel('P(treatment)')
plt.show()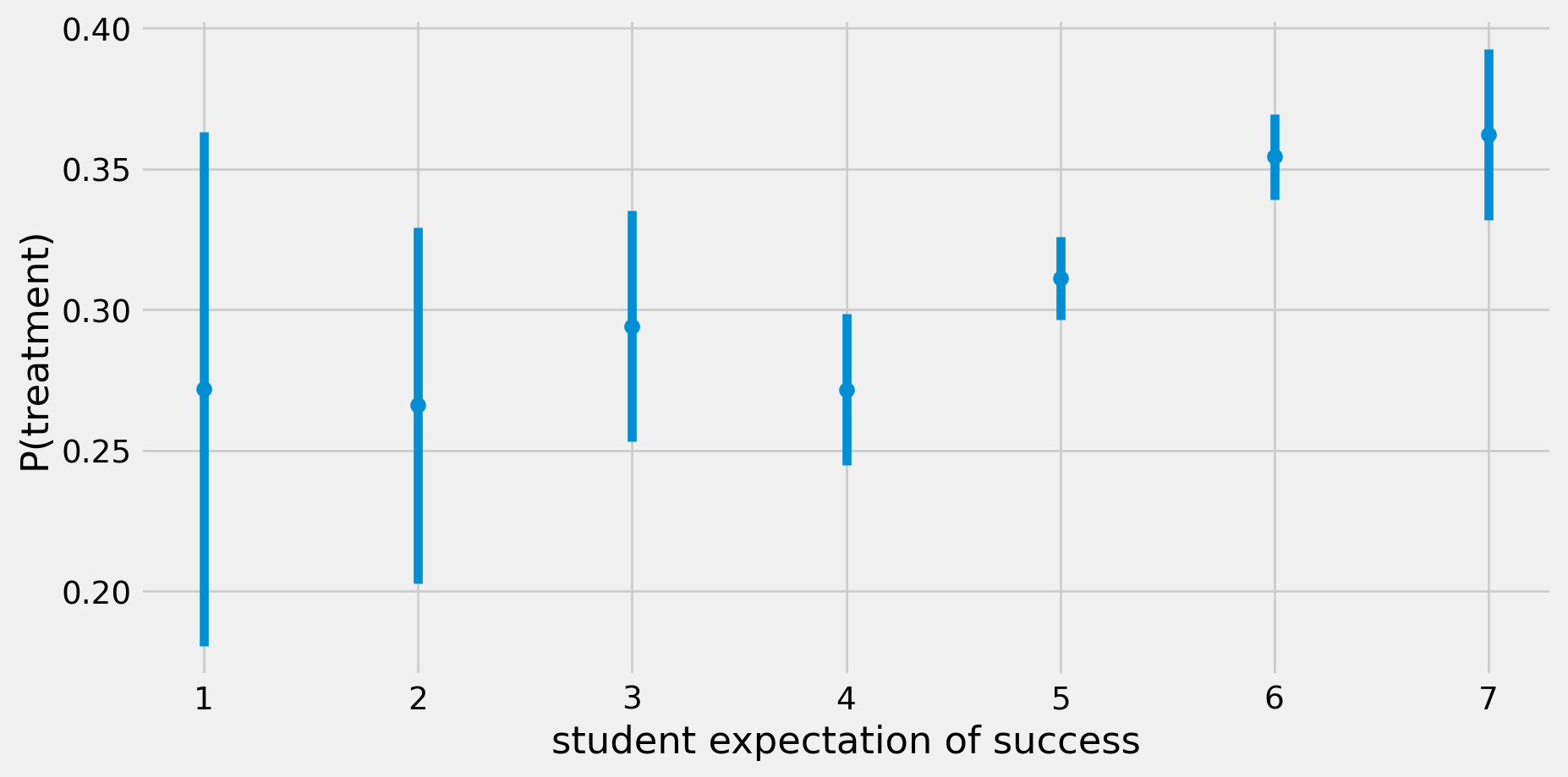

Unadjusted estimate of ATE

print(smf.ols("achievement_score ~ intervention", data=data).fit(cov_type="HC3").summary().tables[1])
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
Intercept       -0.1538      0.012    -13.289      0.000      -0.176      -0.131
intervention     0.4723      0.021     22.968      0.000       0.432       0.513
================================================================================
print(smf.ols("achievement_score ~ intervention", data=data).fit(
    cov_type="cluster", cov_kwds={'groups': data['schoolid']}).summary().tables[1])
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
Intercept       -0.1538      0.036     -4.275      0.000      -0.224      -0.083
intervention     0.4723      0.025     19.184      0.000       0.424       0.521
================================================================================

Unadjusted estimate of ATE

Code 
fig,ax=plt.subplots()
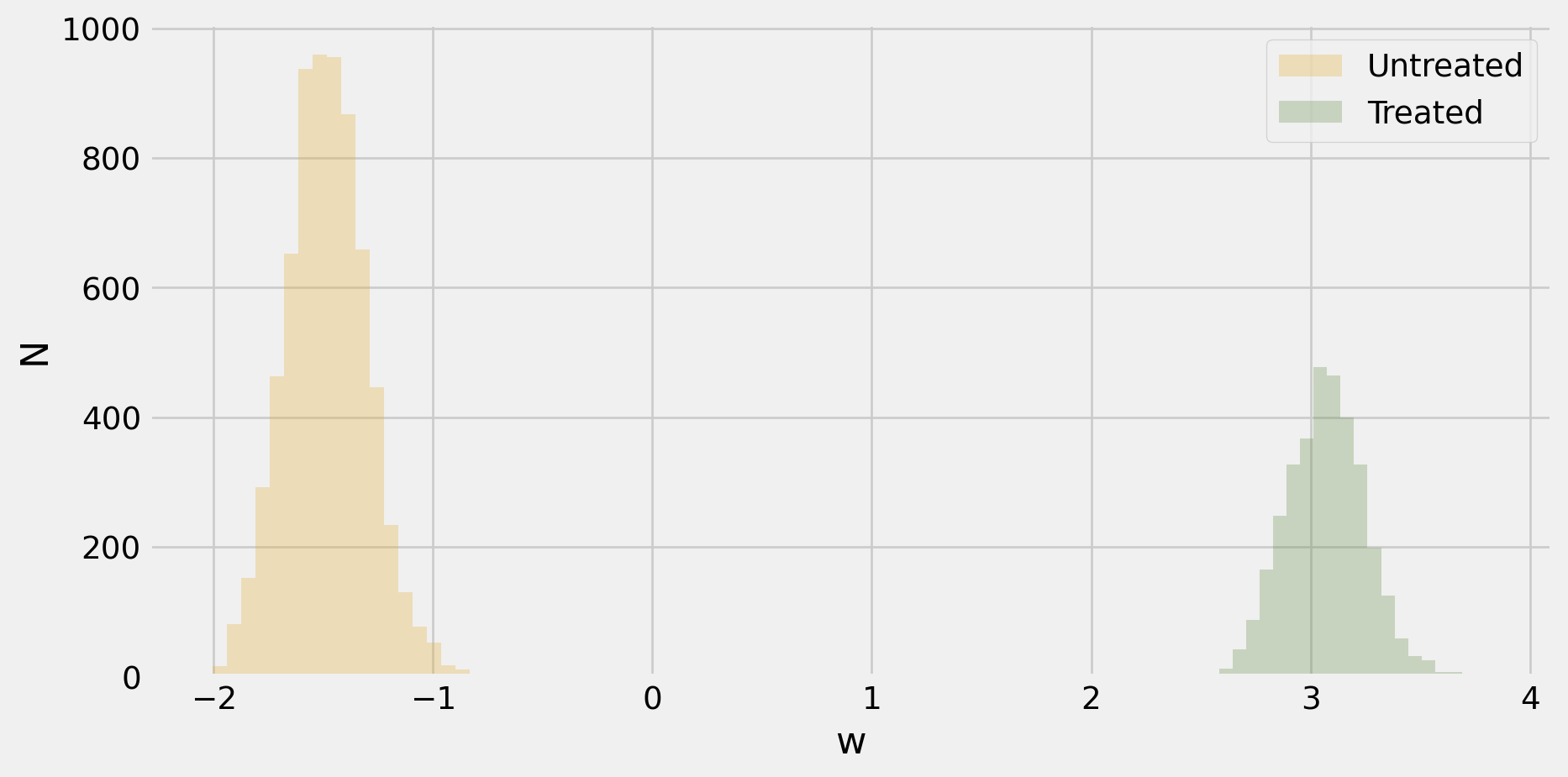
plt.hist(data.query("intervention==0")["achievement_score"], bins=20, alpha=0.3, color="C2")
plt.hist(data.query("intervention==1")["achievement_score"], bins=20, alpha=0.3, color="C3")
plt.vlines(-0.1538, 0, 300, label="Untreated", color="C2")
plt.vlines(-0.1538+0.4723, 0, 300, label="Treated", color="C3")
ax.set_xlabel("Achievement Score")
ax.set_ylabel("N")
plt.legend()
plt.show();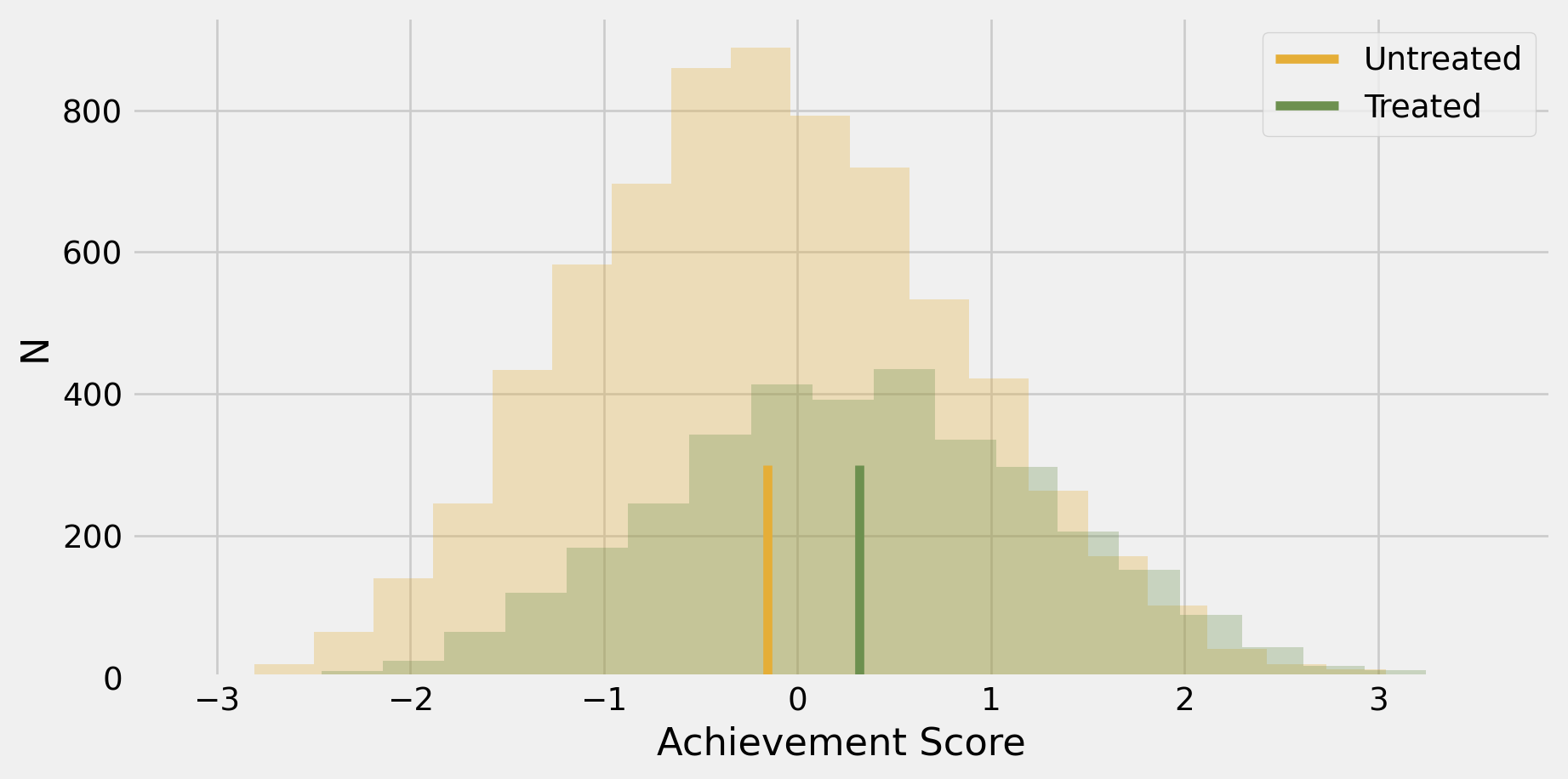

Regression estimate of ATE

ols = smf.ols("achievement_score ~ intervention + success_expect + ethnicity + gender + frst_in_family + school_urbanicity + school_mindset + school_achievement + school_ethnic_minority + school_poverty + school_size",data=data).fit(cov_type="cluster", cov_kwds={'groups': data['schoolid']})
print(ols.summary().tables[1])
==========================================================================================
                             coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------------------
Intercept                 -1.7786      0.110    -16.214      0.000      -1.994      -1.564
intervention               0.3964      0.025     15.558      0.000       0.346       0.446
success_expect             0.3746      0.009     41.120      0.000       0.357       0.392
ethnicity                  0.0043      0.003      1.639      0.101      -0.001       0.009
gender                    -0.2684      0.016    -16.299      0.000      -0.301      -0.236
frst_in_family            -0.1310      0.019     -6.770      0.000      -0.169      -0.093
school_urbanicity          0.0573      0.036      1.613      0.107      -0.012       0.127
school_mindset            -0.1484      0.044     -3.341      0.001      -0.235      -0.061
school_achievement        -0.0253      0.055     -0.457      0.647      -0.134       0.083
school_ethnic_minority     0.1197      0.034      3.471      0.001       0.052       0.187
school_poverty            -0.0154      0.054     -0.284      0.776      -0.122       0.091
school_size               -0.0467      0.044     -1.060      0.289      -0.133       0.040
==========================================================================================

Regression estimate of ATE: weights

lpm = smf.ols("intervention ~ success_expect + ethnicity + gender + frst_in_family + school_urbanicity + school_mindset + school_achievement + school_ethnic_minority + school_poverty + school_size",data=data).fit(cov_type="cluster", cov_kwds={'groups': data['schoolid']})
w = lpm.resid / np.var(lpm.resid)
print(np.mean(data.achievement_score*w))
0.39640236033389553

Regression estimate of ATE: weights

Code 
fig,ax=plt.subplots()
plt.hist(w[data.intervention==0], bins=20, alpha=0.3, color="C2", label="Untreated")
plt.hist(w[data.intervention==1], bins=20, alpha=0.3, color="C3", label="Treated")
ax.set_xlabel("w")
ax.set_ylabel("N")
plt.legend()
plt.show();

Propensity Score Matching

categ = ["ethnicity", "gender", "school_urbanicity","success_expect"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]

data_with_categ = pd.concat([
    data.drop(columns=categ), # dataset without the categorical features
    pd.get_dummies(data[categ], columns=categ, drop_first=False)# categorical features converted to dummies
], axis=1)

print(data_with_categ.shape)
T = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])
(10391, 38)

Propensity Score Matching

from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.neighbors import KNeighborsRegressor
import sklearn

def propensitymatching(T,Y,X,psmodel=LogisticRegressionCV(scoring='neg_log_loss'),neighbormodel=KNeighborsRegressor(n_neighbors=1,algorithm='auto',weights='uniform')):
    pfit = psmodel.fit(X,T)
    ps = pfit.predict_proba(X)[:,1]
    ey1 = neighbormodel.fit(ps[T==1].reshape(-1,1),Y[T==1])
    ey0 = sklearn.base.clone(neighbormodel).fit(ps[T==0].reshape(-1,1),Y[T==0])
    tex = ey1.predict(ps.reshape(-1,1)) - ey0.predict(ps.reshape(-1,1))
    ate = np.mean(tex)
    return(ate, tex,ps)

ate,tex,ps=propensitymatching(data_with_categ[T],data_with_categ[Y],data_with_categ[X])
print(ate)
0.4163456073819457

Propensity Score Matching

Code 
fig, ax = plt.subplots(2,1)
treat = data.intervention
ax[0].scatter(ps[treat==0],tex[treat==0],color="C2")
ax[0].scatter(ps[treat==1],tex[treat==1],color="C3")
ax[1].hist(ps[treat==0],bins=20,color="C2",label="Untreated")
ax[1].hist(ps[treat==1],bins=20,color="C3",label="Treated")
ax[1].set_xlabel("P(Treatment)")
ax[1].set_ylabel("N")
ax[0].set_ylabel("E[Y|T=1,P(X)] - E[Y|T=0,P(X)]")
plt.legend()
plt.show()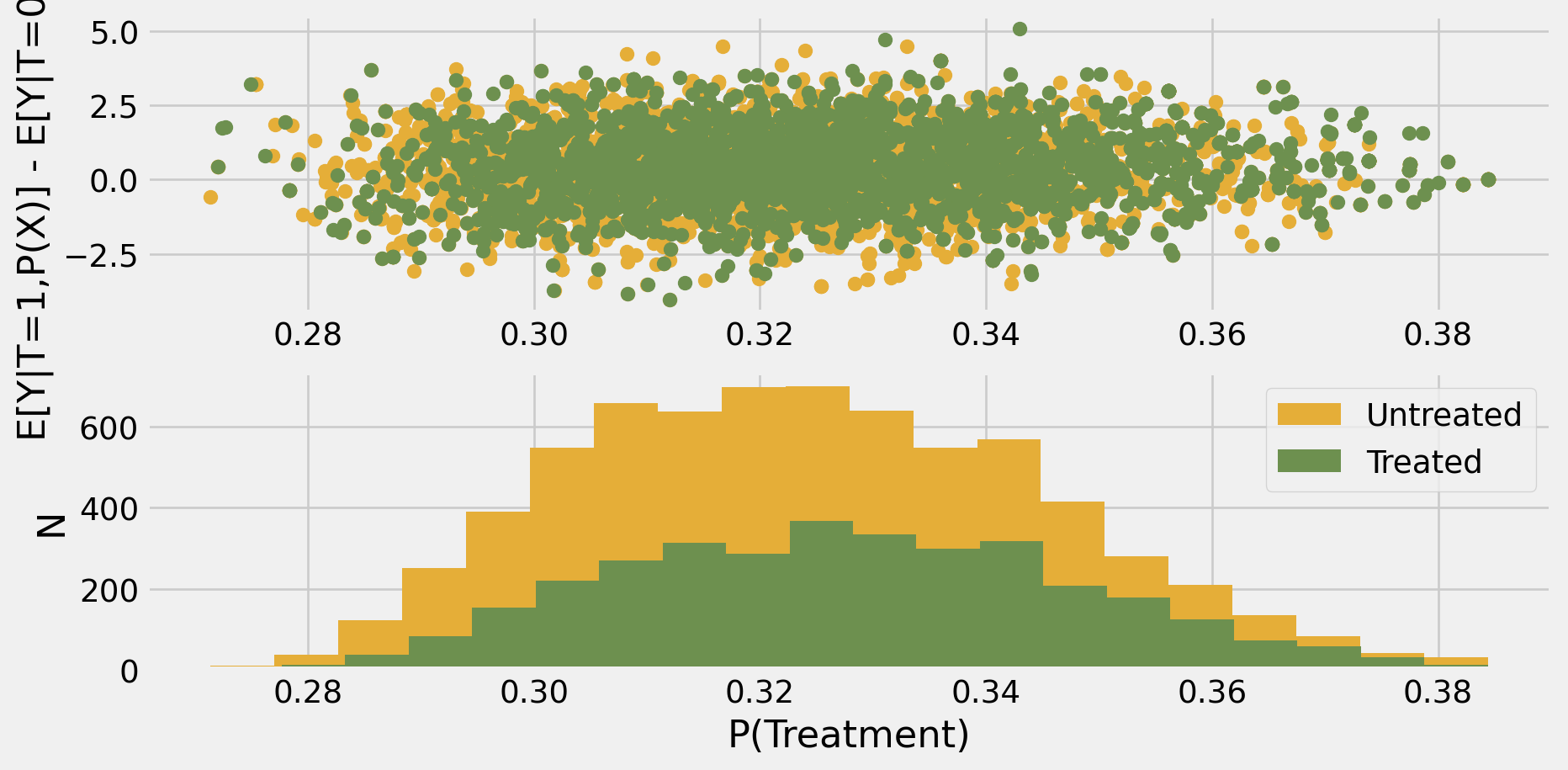

Inverse Propensity Weighting

def ipw(T,Y,X,psmodel=LogisticRegressionCV(scoring='neg_log_loss')):
    pfit = psmodel.fit(X,T)
    ps = pfit.predict_proba(X)[:,1]
    ate=np.mean(Y*(T - ps)/(ps*(1-ps)))
    return(ate,ps)

ate,ps = ipw(data_with_categ[T],data_with_categ[Y],data_with_categ[X])
print(ate)
0.44256557543538383

Doubly Robust

from sklearn.ensemble import GradientBoostingRegressor, GradientBoostingClassifier
from sklearn.linear_model import LassoCV, LogisticRegressionCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures

def robustate(T,Y,X,psmodel=LogisticRegressionCV(scoring='neg_log_loss'),ymodel=LassoCV(), cluster=None):
    pfit = psmodel.fit(X,T)
    ps = pfit.predict_proba(X)[:,1]
    ey1fit = ymodel.fit(X[T==1],Y[T==1])
    ey0fit = sklearn.base.clone(ymodel).fit(X[T==0],Y[T==0])
    ey1 = ey1fit.predict(X)
    ey0 = ey0fit.predict(X)
    ate_terms = ey1 - ey0 + T*(Y- ey1)/ps - (1-T)*(Y-ey0)/(1-ps)
    ate = np.mean(ate_terms)
    # check if cluster is None
    if cluster is None :
        ate_se = np.sqrt(np.var(ate_terms)/len(ate_terms))
    else :
        creg=smf.ols("y ~ 1", pd.DataFrame({"y" : ate_terms})).fit(cov_type="cluster", cov_kwds={'groups': cluster})
        ate_se = np.sqrt(creg.cov_params().iloc[0,0])

    return(ate, ate_se, ps, ey1,ey0)

ate,se,ps,ey1,ey0 = robustate(data_with_categ[T],data_with_categ[Y],data_with_categ[X],cluster=data_with_categ['schoolid'])
print(ate-1.96*se, ate, ate+1.96*se)
0.3317146398974234 0.3832790165781086 0.4348433932587938

1

Doubly Robust

  • better to use the doubleml package
import doubleml as dml

m = LassoCV()
g = LogisticRegressionCV(scoring='neg_log_loss')
dmldata = dml.DoubleMLData(data_with_categ, Y,T,X.to_list())
dmlATE = dml.DoubleMLAPOS(dmldata, m, g, treatment_levels=[0, 1])
dmlATE.fit()
dmlATE.summary
dmlATE.causal_contrast(0).summary
coef std err t P>|t| 2.5 % 97.5 %
1 vs 0 0.382427 0.017134 22.319628 0.0 0.348844 0.416009

Sources and Further Reading

  • Useful additional reading is chapters 10-12 of Facure (2022) and chapter 14 of Huntington-Klein (2021).1

  • Chapters 5 and 10 of Chernozhukov et al. (2024)

  • The representation of the estimate from a linear model as a weighted average is based on Borusyak and Jaravel (2018)

  • The growth mindset example is take from Facure (2022)

References

Abadie, Alberto, and Guido W. Imbens. 2008. “On the Failure of the Bootstrap for Matching Estimators.” Econometrica 76 (6): 1537–57. https://doi.org/https://doi.org/10.3982/ECTA6474.
Athey, Susan, and Stefan Wager. 2019. “Estimating Treatment Effects with Causal Forests: An Application.”
Borusyak, Kirill, and Xavier Jaravel. 2018. “Revisiting Event Study Designs.” https://scholar.harvard.edu/files/borusyak/files/borusyak_jaravel_event_studies.pdf.
Chernozhukov, V., C. Hansen, N. Kallus, M. Spindler, and V. Syrgkanis. 2024. Applied Causal Inference Powered by ML and AI. https://causalml-book.org/.
Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.
Huntington-Klein, Nick. 2021. The Effect: An Introduction to Research Design and Causality. CRC Press. https://theeffectbook.net/.
Yeager, David S., Paul Hanselman, Gregory M. Walton, Jared S. Murray, Robert Crosnoe, Chandra Muller, Elizabeth Tipton, et al. 2019. “A National Experiment Reveals Where a Growth Mindset Improves Achievement.” Nature 573 (7774): 364–69. https://doi.org/10.1038/s41586-019-1466-y.