Regression Discontinuity

ECON526

Paul Schrimpf
paul.schrimpf@ubc.ca

University of British Columbia

Introduction

\[ \def\indep{\perp\!\!\!\perp} % \def\idp{\perp\kern-5pt\perp} \def\Er{\mathrm{E}} \def\var{\mathrm{Var}} \def\cov{\mathrm{Cov}} \def\R{\mathbb{R}} \def\En{{\mathbb{E}_n}} \def\Pr{\mathrm{P}} \newcommand{\norm}[1]{\left\Vert {#1} \right\Vert} \newcommand{\abs}[1]{\left\vert {#1} \right\vert} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]

Sharp Discontinuity

Regression Discontinuity

  • Treatment \(D_i \in \{0,1\}\)
  • Potential outcomes \(Y_i(d)\)
  • Running variable \(R_i\), treatment assignment discontinuous in \(r\) at cutoff \(c\)
    • Sharp: \(P(D|R)\) jumps from 0 to 1
    • Fuzzy: \(P(D|R)\) jumps
Code 
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('tableau-colorblind10')

def pdr(r):
    if (r < 0):
        return 0 #0.2/(1+np.exp(-r))
    else:
        return 1 # 0.8/(1+0.5*np.exp(-r))

def plotp(ax, pdr):
    r = np.linspace(-2,2,500)
    ax.plot(r, list(map(pdr,r)), color='C0')
    ax.set_xlabel('R')
    ax.set_ylabel('Pr(D=1|R)')
    return(ax)
fig, ax = plt.subplots(figsize=(5,5))
ax = plotp(ax,pdr)

Running Variables and Discontinuities

  • Usually come from institutional rules
  • Treatment / program eligibility changes discretely with \(R\)
  • Common running variables:
    • Geographic location
    • Income, wealth
    • Test scores
    • Votes
    • Age

Continuous Potential Outcomes

  • Assume continuity: \[\Er[Y(1)|R=r]\] and \[\Er[Y(0)|R=r]\] are continuous in \(r\)
  • Observed \[ \begin{align*} \Er[Y|R] = & \Pr(D=1|R)\Er[Y(1)|R,D=1] + \\ & + \Pr(D=0|R)\Er[Y(0)|R,D=0] \end{align*} \]
  • Idea: size of discontinuity in \(\Er[Y|R]\) is related to a treatment effect
Code 
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('tableau-colorblind10')

def Ey(d,r) :
    if d < 0.1 :
        return 0.5*(r+0.2)**3 + 0.1*(r+0.2)**2
    else :
        return 2 + 0.3*r**3 + r

fig, ax = plt.subplots(2,1, figsize=(4,7))
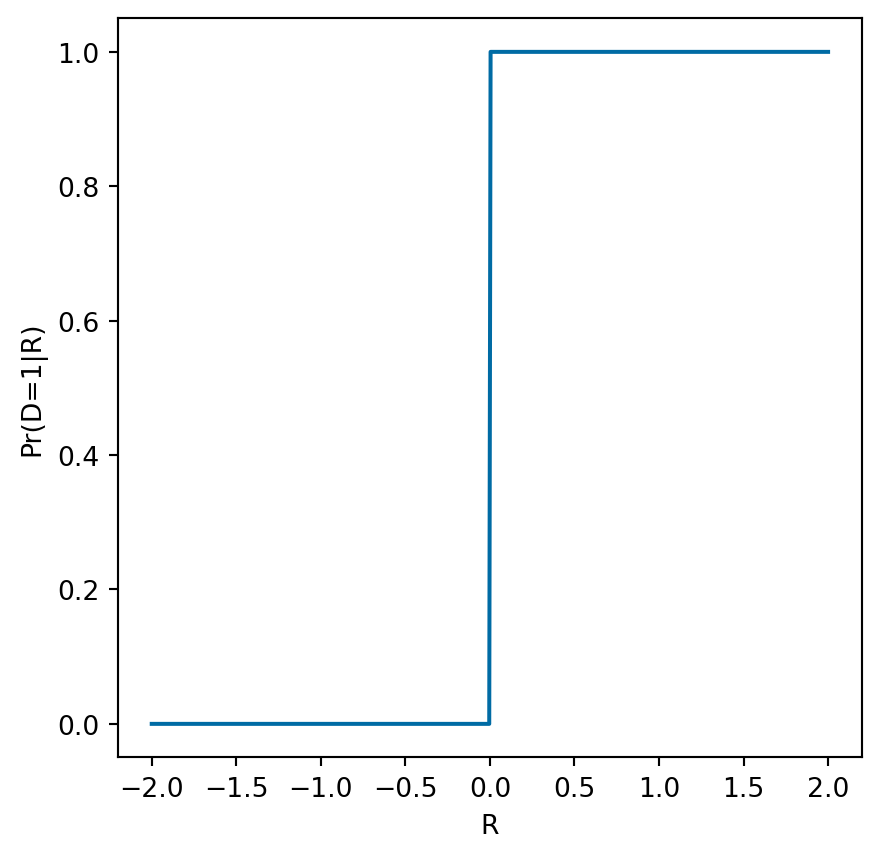
ax[0] = plotp(ax[0],pdr)

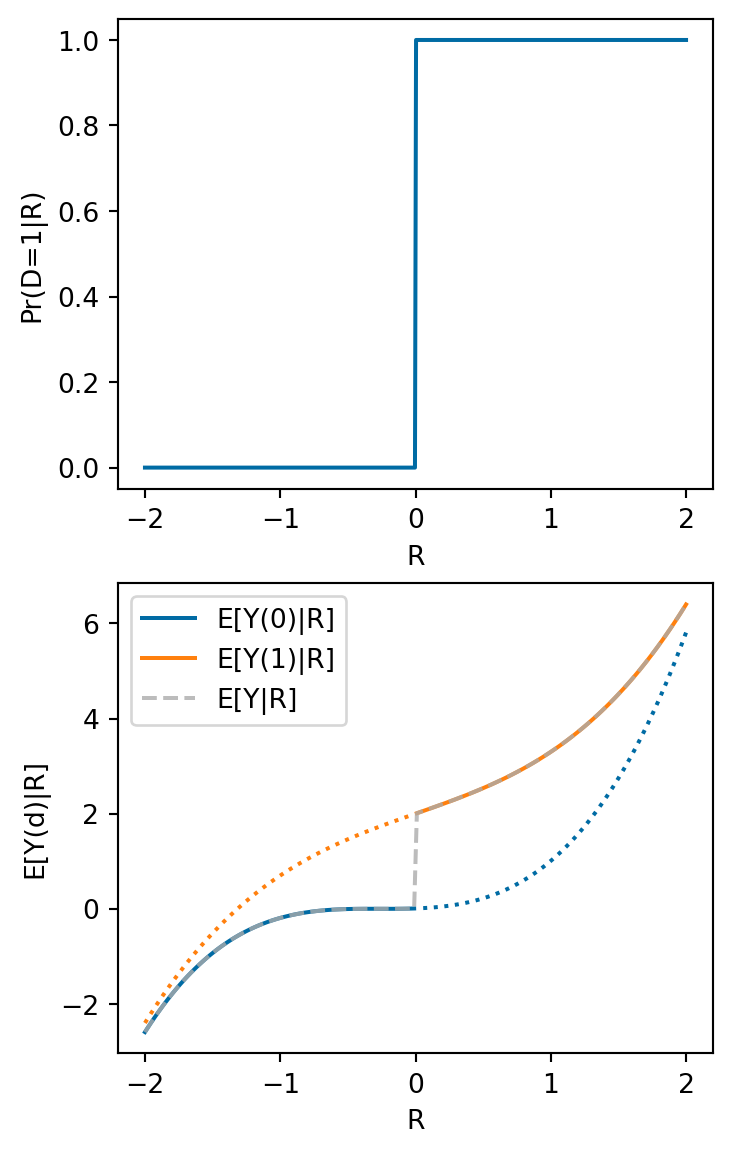
def plotey(ax,Ey,pdr) :
    r = np.linspace(-2,-0.01,100)
    ax.plot(r, list(map(lambda r: Ey(0,r),r)), color='C0', label="E[Y(0)|R]")
    r = np.linspace(2,0.01,100)
    ax.plot(r, list(map(lambda r: Ey(0,r),r)), color='C0', linestyle=":")
    r = np.linspace(-2,-0.01,100)
    ax.plot(r, list(map(lambda r: Ey(1,r),r)), color='C1', linestyle=":")
    r = np.linspace(2,0.01,100)
    ax.plot(r, list(map(lambda r: Ey(1,r),r)), color='C1', label="E[Y(1)|R]")
    r = np.linspace(-2,2,200)
    ax.plot(r,list(map(lambda r: pdr(r)*Ey(1,r) + (1-pdr(r))*Ey(0,r),r)), color='C2', label="E[Y|R]", linestyle="--", alpha=0.8)
    ax.legend()
    ax.set_xlabel('R')
    ax.set_ylabel('E[Y(d)|R]')
    return(ax)

ax[1] = plotey(ax[1],Ey,pdr)

Identification

  • Size of disconuity in \(\Er[Y|R]\) \[ \begin{align*} \lim_{r \downarrow c} \Er[Y|R=r] - \lim_{r \uparrow c} \Er[Y|R=r] & = \lim_{r \downarrow c} \Er[Y(1)|R=r] - \lim_{r \uparrow c} \Er[Y(0),r)|R=r] \\ & = \Er[Y(1) - Y(0) | R=c] \end{align*} \]
  • Identifies ATE conditional on being at the cutoff
  • Assuming:
    1. Sharp discontinuity \(P(D|R=r) = \begin{cases} 0 & \; r<c \\ 1 & r \geq c \end{cases}\)
    2. Continuity of \(\Er[Y(1)|R=r]\) and \(\Er[Y(0)|R=r]\)

Data

Code 
n = 1_000
sig = 2
fig,ax=plt.subplots()
r = np.random.rand(n)*4-2
y = np.vectorize(lambda r: Ey(np.sign(r)*2+1,r) + np.random.randn()*sig)(r)
ax =plotey(ax,Ey,pdr)
ax.scatter(r,y,color='C2', alpha=0.5,s=1)
plt.show()

Estimation

  • Fit regression to left and right of discontinuity using only observations near the cutoffs
import pandas as pd
import statsmodels.formula.api as smf
from statsmodels.iolib.summary2 import summary_col

df = pd.DataFrame({'y':y,'r':r})

def rdd(df, h, c=0, R='r', Y='y') :
    wdf = df.loc[np.abs(df[R]-c)<=h]
    m=smf.ols(f'{Y} ~ I({R}-c)*I({R}>c)',wdf).fit(cov_type="HC3")
    return(m)

bandwidths=[.25, 0.5, 1., 2.]
models = [rdd(df,h) for h in bandwidths]
summary_col(models, model_names=[f"h={h:.2}" for h in bandwidths])

Estimation

h=0.25 h=0.5 h=1.0 h=2.0
Intercept 0.4863 0.9287 0.6551 0.5983
(0.5177) (0.3872) (0.2677) (0.1910)
I(r > c)[T.True] 3.1391 1.0377 1.3319 0.6969
(0.8266) (0.6178) (0.3905) (0.2704)
I(r - c) -2.3451 2.8042 1.3378 1.0197
(3.8122) (1.3789) (0.4447) (0.1652)
I(r - c):I(r > c)[T.True] -9.2769 -2.0312 -0.4992 1.1414
(5.3322) (2.1534) (0.6495) (0.2293)
R-squared 0.1409 0.1960 0.2851 0.5434
R-squared Adj. 0.1164 0.1851 0.2807 0.5420

Standard errors in parentheses.

Plotting Estimates

def plotrdd(ax,df, h, c=0, R='r',Y='y', Ey=Ey) :
    df = df.sort_values(R)
    m = rdd(df,h,c,R,Y)
    df.plot.scatter(x=R,y=Y,ax=ax,color="C2",alpha=0.5,s=1)
    df.assign(predictions=m.fittedvalues).plot(x=R, y="predictions",label='Estimate', ax=ax, color="C3")
    df.assign(Ey0=df[R].apply(lambda r: Ey(0,r))).plot(x=R,y='Ey0',label="E[Y(0)|R]",ax=ax,color="C0",linestyle="--")
    df.assign(Ey1=df[R].apply(lambda r: Ey(1,r))).plot(x=R,y='Ey1',label="E[Y(1)|R]",ax=ax,color="C1",linestyle="--")
    #ax.get_legend().remove()
    return(ax)

fig,ax = plt.subplots(2,2, figsize=(10,5))
for (i,h) in enumerate(bandwidths) :
    plotrdd(ax.flat[i],df,h)
    ax.flat[i].set_title(f"h={h:.2}")

Plotting Estimates

Questions

  • Is there a better way to visualize?
  • How to choose h?
  • Are these standard errors correct?
  • Are there any falsification or other checks to do?

Binned Scatter Plot

  • Divide range of \(R\) into bins, plot mean within each bin
  • Many papers just show binned means, but better to show uncertainty / variability in data too
    • Two good options in rdrobust package:
      1. binselect='es' or qs' and plot confidence intervals
      2. binselect='esmv' or 'qsmv'
  • See Cattaneo, Idrobo, and Titiunik (2019) section 3 and Cattaneo et al. (2024)
Code 
import rdrobust
rdp = rdrobust.rdplot(df.y,df.r,c=0,hide=True, binselect='es')
fg,ax=plt.subplots(figsize=(4,6))
pltdf = rdp.vars_bins
pltdf.plot.scatter(x='rdplot_mean_bin',y='rdplot_mean_y', color='black',ax=ax,label='IMSE optimal bins')
ax.set_xlabel('R')
ax.set_ylabel('Y')
ax.errorbar(x=pltdf.rdplot_mean_bin,y=pltdf.rdplot_mean_y,
             yerr=[pltdf.rdplot_mean_y-pltdf.rdplot_ci_l,pltdf.rdplot_ci_r - pltdf.rdplot_mean_y],
             ls='none',color="black")
rdp = rdrobust.rdplot(df.y,df.r,c=0,hide=True, binselect='esmv')
pltdf = rdp.vars_bins
pltdf.plot.scatter(x='rdplot_mean_bin',y='rdplot_mean_y', color='C4',ax=ax,label='Variance mimicking bins')
df.plot.scatter(x='r',y='y',color='C2',s=1,alpha=0.5,label=None,ax=ax)
ax.legend()
plt.show()

Bandwidth Selection

  • Bandwith, h, has bias variance tradeoff
  • Larger h \(\Rightarrow\) lower variance, higher bias
  • Smaller h \(\Rightarrow\) higher variance, lower bias
  • Optimal h balances bias and variance
  • Optimal h will decrease with sample size

Bandwidth Selection

rd = rdrobust.rdrobust(df.y,df.r, kernel="uniform",  bwselect="msetwo")
rd
Call: rdrobust
Number of Observations:                  1000
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                               Uniform
Bandwidth Selection:                   msetwo
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations           475        525
Number of Unique Obs.            475        525
Number of Effective Obs.         133        134
Bandwidth Estimation           0.567      0.603
Bandwidth Bias                 0.972      1.066
rho (h/b)                      0.583      0.565

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       0.905    0.539    1.681   9.278e-02     [-0.15, 1.961]
Robust                 -        -    1.297   1.945e-01    [-0.427, 2.098]

Confidence Intervals

  • Optimal h has \(\mathrm{Bias}^2 = \var\)
  • Need to correct for bias for confidence intervals to be correct
  • Use “Robust” interval reported by rdrobust
  • See section 4.3 of Cattaneo, Idrobo, and Titiunik (2019)

Kernel Weighting

  • Instead of treating all observations within bandwith as equally important for estimating discontinuity, we might want to weight observations closer to discontinuity more
  • “triangular” kernel is best
rd = rdrobust.rdrobust(df.y,df.r, kernel="triangular",  bwselect="msetwo")
rd
Call: rdrobust
Number of Observations:                  1000
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                            Triangular
Bandwidth Selection:                   msetwo
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations           475        525
Number of Unique Obs.            475        525
Number of Effective Obs.         159        147
Bandwidth Estimation           0.673      0.644
Bandwidth Bias                 1.071      1.085
rho (h/b)                      0.629      0.594

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       1.287    0.564    2.283   2.242e-02     [0.182, 2.391]
Robust                 -        -     1.91   5.613e-02    [-0.033, 2.587]

Manipulation of Running Variable

  • If units can change \(R_i\), they might do in way to change treatment status
  • Manipulation of \(R_i\) makes continuity of \(\Er[Y(d)|R]\) less plausible
  • Check for bunching in density of \(R_i\) near cutoff

Manipulation of Running Variable

fig,ax=plt.subplots()
ax.hist(x=df.r[df.r<=0],bins=20,color="C0")
ax.hist(x=df.r[df.r>0],bins=20,color="C1")
ax.set_xlim(-2,2)
ax.axvline(0,color="black")
plt.show()

Placebo Tests

  • If have data on outcomes not affected by treatment (e.g. if predetermined) can check that RD estimate for them is 0
df.x = np.sin(2*df.r)*np.exp(0.5*df.r) + np.random.randn(df.shape[0])
rdx = rdrobust.rdrobust(df.x,df.r, kernel="triangular",  bwselect="msetwo")
rdx
Call: rdrobust
Number of Observations:                  1000
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                            Triangular
Bandwidth Selection:                   msetwo
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations           475        525
Number of Unique Obs.            475        525
Number of Effective Obs.         170        131
Bandwidth Estimation           0.726      0.588
Bandwidth Bias                 1.121      1.216
rho (h/b)                      0.648      0.483

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       0.187    0.316    0.593   5.534e-01    [-0.432, 0.806]
Robust                 -        -     0.15   8.810e-01    [-0.653, 0.762]

Placebo Tests

rdpx = rdrobust.rdplot(df.x,df.r,c=0,hide=False, binselect='es',x_label="R",y_label="x",ci=95)

Fuzzy Discontinuity

Fuzzy Discontinuity

  • \(P(D|R)\) discontinuous at \(c\)
  • imperfect compliance
  • Idea: use discontinuity as instrument for treatment
Code 
def pdr(r):
    if (r < 0):
        return 0.2/(1+np.exp(-r))
    else:
        return 0.8/(1+0.5*np.exp(-r))

fig, ax = plt.subplots(figsize=(5,5))
ax = plotp(ax,pdr)

Merit Based Financial Aid for Low-Income Students

  • Londoño-Vélez, Rodríguez, and Sánchez (2020) (also used as example in Cattaneo, Idrobo, and Titiunik (2024))
  • Full undergraduate tuition available if
    1. Standardized test \(\geq\) 91%-tile
    2. Wealth index \(\leq\) cutoff(region)
  • Two discontinuities
  • Outcome \(=\) postsecondary enrollment
  • Focus on wealth cutoff

Merit Based Financial Aid for Low-Income Students

lrs_all = pd.read_stata('data/data_RD.dta')
lrs = lrs_all.loc[lrs_all.eligible_saber11==1] #
lrs.columns
Index(['running_saber11_placebo', 'running_saber11', 'running_sisben',
       'eligible_saber11', 'eligible_sisben', 'eligible_spp', 'sisben_area',
       'sisben_score', 'beneficiary_spp', 'spadies_any', 'spadies_hq',
       'spadies_lq', 'spadies_hq_pub', 'spadies_hq_pri', 'spadies_lq_pub',
       'spadies_lq_pri', 'spadies_hq_id', 'icfes_per', 'icfes_female',
       'icfes_age', 'icfes_urm', 'icfes_stratum', 'icfes_stratum1',
       'icfes_stratum2', 'icfes_stratum3', 'icfes_stratum4', 'icfes_stratum5',
       'icfes_stratum6', 'icfes_educm1', 'icfes_educm2', 'icfes_educm3',
       'icfes_educm4', 'icfes_educp1', 'icfes_educp2', 'icfes_educp3',
       'icfes_educp4', 'icfes_famsize', 'icfes_works', 'icfes_privatehs',
       'icfes_schoolsch1', 'icfes_schoolsch2', 'icfes_schoolsch3',
       'icfes_schoolsch4', 'icfes_schoolsch5', 'icfes_score_20132',
       'icfes_score_20142'],
      dtype='object')

First Stage: Effect on Receiving Tuition Subsidy

df=lrs[["running_sisben","beneficiary_spp","icfes_score_20142","spadies_any","spadies_hq"]].dropna()
rdrobust.rdplot(df.beneficiary_spp, df.running_sisben, binselect='esmv', x_label="Wealth Index",y_label="P(D|wealth)")

First Stage: Effect on Receiving Tuition Subsidy

Mass points detected in the running variable.
Warning: not enough variability in the outcome variable below the threshold

Call: rdplot
Number of Observations:                 23132
Kernel:                               Uniform
Polynomial Order Est. (p):                  4

                                Left      Right
------------------------------------------------
Number of Observations          7709      15423
Number of Effective Obs         7709      15423
Bandwith poly. fit (h)         43.48      56.23
Number of bins scale               1          1
Bins Selected                      1        234
Average Bin Length             43.48       0.24
Median Bin Length              43.48       0.24
IMSE-optimal bins                nan        8.0
Mimicking Variance bins          nan      234.0

Relative to IMSE-optimal:
Implied scale                    nan      29.25
WIMSE variance weight            nan        0.0
WIMSE bias weight                nan        1.0

First Stage: Effect on Receiving Tuition Subsidy

fs = rdrobust.rdrobust(df.beneficiary_spp, df.running_sisben, kernel="triangular",  bwselect="mserd")
fs
Mass points detected in the running variable.
Mass points detected in the running variable.
Call: rdrobust
Number of Observations:                 23132
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                            Triangular
Bandwidth Selection:                    mserd
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations          7709      15423
Number of Unique Obs.           3644       9327
Number of Effective Obs.        6600       7466
Bandwidth Estimation           18.51      18.51
Bandwidth Bias                28.994     28.994
rho (h/b)                      0.638      0.638

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       0.625    0.012   51.592   0.000e+00     [0.601, 0.649]
Robust                 -        -   43.114   0.000e+00     [0.595, 0.652]

Reduced Form: Effect on Postsecondary Enrollment

rdrobust.rdplot(df.spadies_any, df.running_sisben, binselect='esmv', x_label="Wealth Index",y_label="P(postsecondary|wealth)")

Reduced Form: Effect on Postsecondary Enrollment

Mass points detected in the running variable.

Call: rdplot
Number of Observations:                 23132
Kernel:                               Uniform
Polynomial Order Est. (p):                  4

                                Left      Right
------------------------------------------------
Number of Observations          7709      15423
Number of Effective Obs         7709      15423
Bandwith poly. fit (h)         43.48      56.23
Number of bins scale               1          1
Bins Selected                    232        238
Average Bin Length             0.196      0.236
Median Bin Length              0.187      0.236
IMSE-optimal bins                5.0        9.0
Mimicking Variance bins        232.0      238.0

Relative to IMSE-optimal:
Implied scale                   46.4     26.444
WIMSE variance weight            0.0        0.0
WIMSE bias weight                1.0        1.0

Reduced Form: Effect on Postsecondary Enrollment

rf = rdrobust.rdrobust(df.spadies_any, df.running_sisben, kernel="triangular",  bwselect="mserd")
rf
Mass points detected in the running variable.
Mass points detected in the running variable.
Call: rdrobust
Number of Observations:                 23132
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                            Triangular
Bandwidth Selection:                    mserd
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations          7709      15423
Number of Unique Obs.           3644       9327
Number of Effective Obs.        3877       3908
Bandwidth Estimation           9.042      9.042
Bandwidth Bias                14.404     14.404
rho (h/b)                      0.628      0.628

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       0.269    0.023   11.709   1.144e-31     [0.224, 0.314]
Robust                 -        -   10.048   9.410e-24     [0.221, 0.328]

Questions

  • How to get an IV estimate?
  • What causal interpretation can we give an IV estimate?

Potential Outcomes

  • “Assigned treatment \(A_i = 1\{R_i > c\}\)
  • Potential treatments \(D_i(A_i) \in \{0,1\}\)
  • Potential outcomes \(Y_i(a, d)\)
  • Observed outcome \(Y_i(A_i,D_i(A_i))\)
  • Exclusion restriction: \(R_i\) does not affect treatment or outcome, except through \(A_i\)

LATE

  • Assume monotonicity: \(D_i(1) \geq D_i(0)\) \[ \frac{\text{reduced form}}{\text{first stage}} \inprob \Er[Y(1) - Y(0) | wealth=c_w, test>c_t, D_i(1)>D_i(0)] \]
  • Optimal bandwidth choice different
  • Use rdrobust for bandwidth selection and confidence intervals

LATE

late = rdrobust.rdrobust(df.spadies_any, df.running_sisben, fuzzy=df.beneficiary_spp)
late
Mass points detected in the running variable.
Mass points detected in the running variable.
Call: rdrobust
Number of Observations:                 23132
Polynomial Order Est. (p):                  1
Polynomial Order Bias (q):                  2
Kernel:                            Triangular
Bandwidth Selection:                    mserd
Var-Cov Estimator:                         NN

                                Left      Right
------------------------------------------------
Number of Observations          7709      15423
Number of Unique Obs.           3644       9327
Number of Effective Obs.        3877       3908
Bandwidth Estimation           9.042      9.042
Bandwidth Bias                14.404     14.404
rho (h/b)                      0.628      0.628

Method             Coef.     S.E.   t-stat    P>|t|       95% CI      
-------------------------------------------------------------------------
Conventional       0.434    0.034   12.773   2.322e-37     [0.368, 0.501]
Robust                 -        -   11.026   2.856e-28     [0.366, 0.524]

Sources and Further Reading

  • Facure (2022) chapter 16
  • Chernozhukov et al. (2024) chapter 17
  • Cattaneo, Idrobo, and Titiunik (2019) and Cattaneo, Idrobo, and Titiunik (2024)
  • https://rdpackages.github.io/

References

Cattaneo, Matias D., Richard K. Crump, Max H. Farrell, and Yingjie Feng. 2024. “On Binscatter.” American Economic Review 114 (5): 1488–1514. https://doi.org/10.1257/aer.20221576.
Cattaneo, Matias D., Nicolas Idrobo, and Rocío Titiunik. 2024. A Practical Introduction to Regression Discontinuity Designs: Extensions. Cambridge University Press. https://doi.org/10.1017/9781009441896.
Cattaneo, Matias D., Nicolás Idrobo, and Rocío Titiunik. 2019. A Practical Introduction to Regression Discontinuity Designs: Foundations. Cambridge University Press. https://doi.org/10.1017/9781108684606.
Chernozhukov, V., C. Hansen, N. Kallus, M. Spindler, and V. Syrgkanis. 2024. Applied Causal Inference Powered by ML and AI. https://causalml-book.org/.
Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.
Londoño-Vélez, Juliana, Catherine Rodríguez, and Fabio Sánchez. 2020. “Upstream and Downstream Impacts of College Merit-Based Financial Aid for Low-Income Students: Ser Pilo Paga in Colombia.” American Economic Journal: Economic Policy 12 (2): 193–227. https://doi.org/10.1257/pol.20180131.