Synthetic Control

ECON526

Paul Schrimpf

University of British Columbia

Introduction

\[ \def\Er{{\mathrm{E}}} \def\En{{\mathbb{E}_n}} \def\cov{{\mathrm{Cov}}} \def\var{{\mathrm{Var}}} \def\R{{\mathbb{R}}} \newcommand\norm[1]{\left\lVert#1\right\rVert} \def\rank{{\mathrm{rank}}} \newcommand{\inpr}{ \overset{p^*_{\scriptscriptstyle n}}{\longrightarrow}} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \]

Setup

  • 1 treated unit, observed \(T_0\) periods before treatment, \(T_1\) periods after
  • \(J\) untreated units
  • \(J\), \(T_0\) moderate in size
  • Formalisation of comparative case study

Example: California Tobacco Control Program

  • Code and copy of data from Facure (2022)
  • Data used in Abadie, Diamond, and Hainmueller (2010)
Code 
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf

pd.set_option("display.max_columns", 20)
style.use("fivethirtyeight")

Data: California Tobacco Control Program

cigar = pd.read_csv("data/smoking.csv")
cigar.query("california").head()
state year cigsale lnincome beer age15to24 retprice california after_treatment
62 3 1970 123.000000 NaN NaN 0.178158 38.799999 True False
63 3 1971 121.000000 NaN NaN 0.179296 39.700001 True False
64 3 1972 123.500000 9.930814 NaN 0.180434 39.900002 True False
65 3 1973 124.400002 9.955092 NaN 0.181572 39.900002 True False
66 3 1974 126.699997 9.947999 NaN 0.182710 41.900002 True False

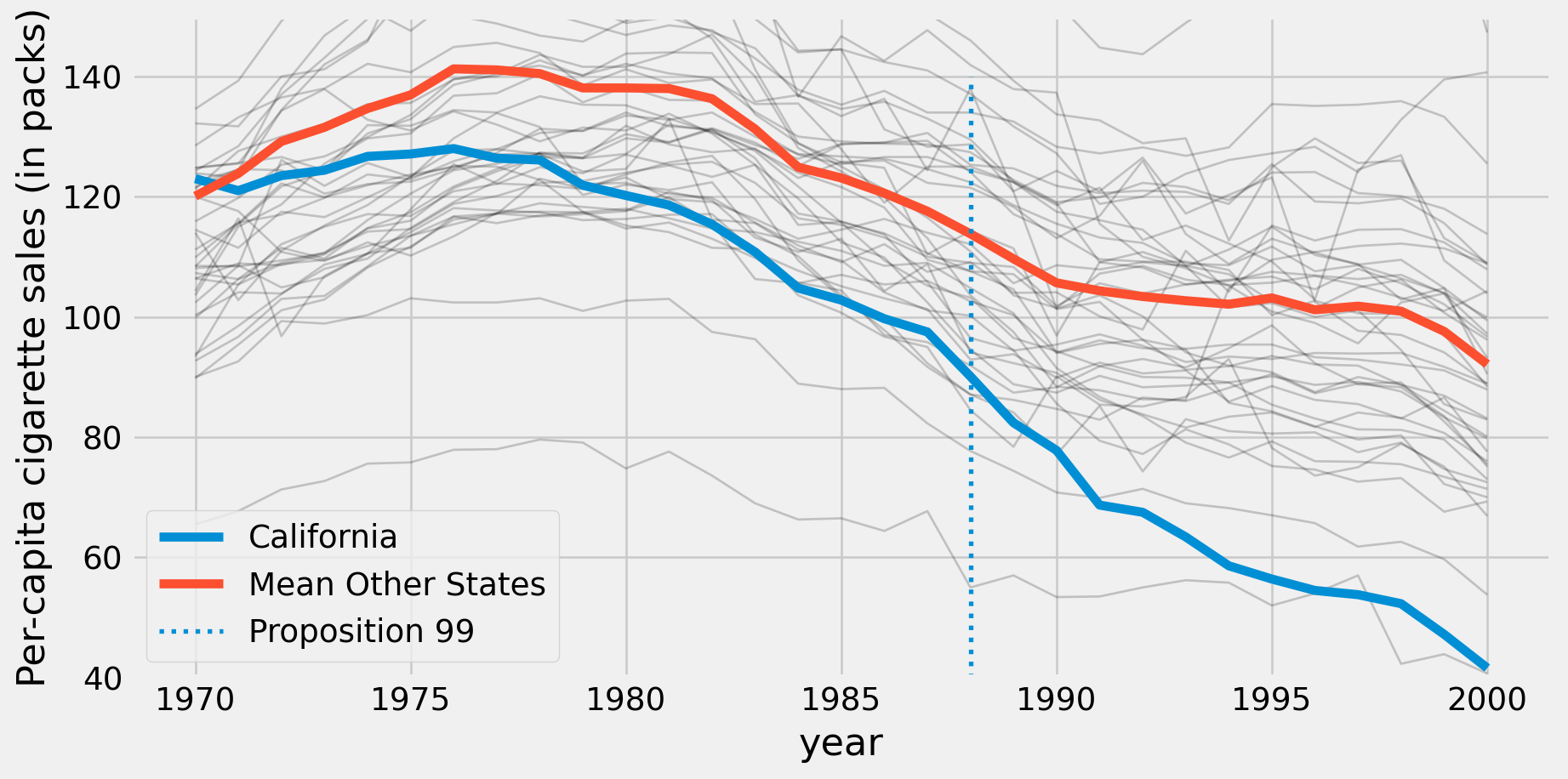
Which Comparison?

  • All states?
  • States bordering California?
  • States with similar characteristics? Which characteristics?

Synthetic Control

  • Compare treated unit (California) to weighted average of untreated units
  • Weights chosen to make sythetic control close to California

Synthetic Control

  • Potential outcomes \(Y_{it}(0), Y_{it}(1)\)
  • For \(t>T_0\), estimate treatment effect on treated unit as \[ \hat{\tau}_{1t} = Y_{1t} - \underbrace{\sum_{j=2}^{J+1} \hat{w}_j Y_{jt}}_{\hat{Y}_{1t}(0)} \]
  • \(\hat{w}_j\) chosen to make synthetic control close to treated unit before treatment

Variables to Match

  • Vector of pretreatment variables for treated unit \[ \mathbf{X}_1 = \left(Y_{11}, \cdots Y_{1T_0}, z_{11}, \cdots, z_1K \right)^T \]
  • Matrix of same variables for untreated \[ \mathbf{X}_0 = \begin{pmatrix} Y_{21} & \cdots & Y_{2T_0} & z_{21} & \cdots & z_{2K} \\ \vdots & & & & & \vdots \\ Y_{J+1,1} & \cdots & Y_{J+1,T_0} & z_{J+1,1} & \cdots & z_{J+1,K} \end{pmatrix}^T \]

Weights

  • Weights minimize difference \[ \begin{align*} \hat{W} = & \textrm{arg}\min_{W \in \R^J} \Vert \mathbf{X}_1 - \mathbf{X}_0 W \Vert_V \\ & s.t. \sum_{j=2}^{J+1} w_j = 1 \\ & \;\;\; 0 \leq w_j \leq 1 \;\; \forall j \end{align*} \]

Computing Weights

features = ["cigsale", "retprice"]
inverted = (cigar.query("~after_treatment") # filter pre-intervention period
            .pivot(index='state', columns="year")[features] # make one column per year and one row per state
            .T) # flip the table to have one column per state
inverted.head()
state 1 2 3 4 5 6 7 8 9 10 ... 30 31 32 33 34 35 36 37 38 39
year
cigsale 1970 89.800003 100.300003 123.000000 124.800003 120.000000 155.000000 109.900002 102.400002 124.800003 134.600006 ... 103.599998 92.699997 99.800003 106.400002 65.500000 122.599998 124.300003 114.500000 106.400002 132.199997
1971 95.400002 104.099998 121.000000 125.500000 117.599998 161.100006 115.699997 108.500000 125.599998 139.300003 ... 115.000000 96.699997 106.300003 108.900002 67.699997 124.400002 128.399994 111.500000 105.400002 131.699997
1972 101.099998 103.900002 123.500000 134.300003 110.800003 156.300003 117.000000 126.099998 126.599998 149.199997 ... 118.699997 103.000000 111.500000 108.599998 71.300003 138.000000 137.000000 117.500000 108.800003 140.000000
1973 102.900002 108.000000 124.400002 137.899994 109.300003 154.699997 119.800003 121.800003 124.400002 156.000000 ... 125.500000 103.500000 109.699997 110.400002 72.699997 146.800003 143.100006 116.599998 109.500000 141.199997
1974 108.199997 109.699997 126.699997 132.800003 112.400002 151.300003 123.699997 125.599998 131.899994 159.600006 ... 129.699997 108.400002 114.800003 114.699997 75.599998 151.800003 149.600006 119.900002 111.800003 145.800003

5 rows × 39 columns

Computing Weights

from scipy.optimize import fmin_slsqp
from toolz import reduce, partial

X1 = inverted[3].values # state of california
X0 = inverted.drop(columns=3).values  # other states

def loss_w(W, X0, X1) -> float:
    return np.sqrt(np.mean((X1 - X0.dot(W))**2))


def get_w(X0, X1):
    w_start = [1/X0.shape[1]]*X0.shape[1]
    weights = fmin_slsqp(partial(loss_w, X0=X0, X1=X1),
                         np.array(w_start),
                         f_eqcons=lambda x: np.sum(x) - 1,
                         bounds=[(0.0, 1.0)]*len(w_start),
                         disp=False)
    return weights

Examining Weights

  • Weights tend to be sparse
  • Good idea to examine which untreated units get positive weight
  • Should look at state names, but the data does not have them, and the state variable is not FIPs code or any standard identifier
calif_weights = get_w(X0, X1)
print("Sum:", calif_weights.sum())
np.round(calif_weights, 4)
Sum: 1.000000000000424
array([0.    , 0.    , 0.    , 0.0852, 0.    , 0.    , 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.113 , 0.1051, 0.4566, 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    ,
       0.2401, 0.    , 0.    , 0.    , 0.    , 0.    ])

Effect of California Tobacco Control Program

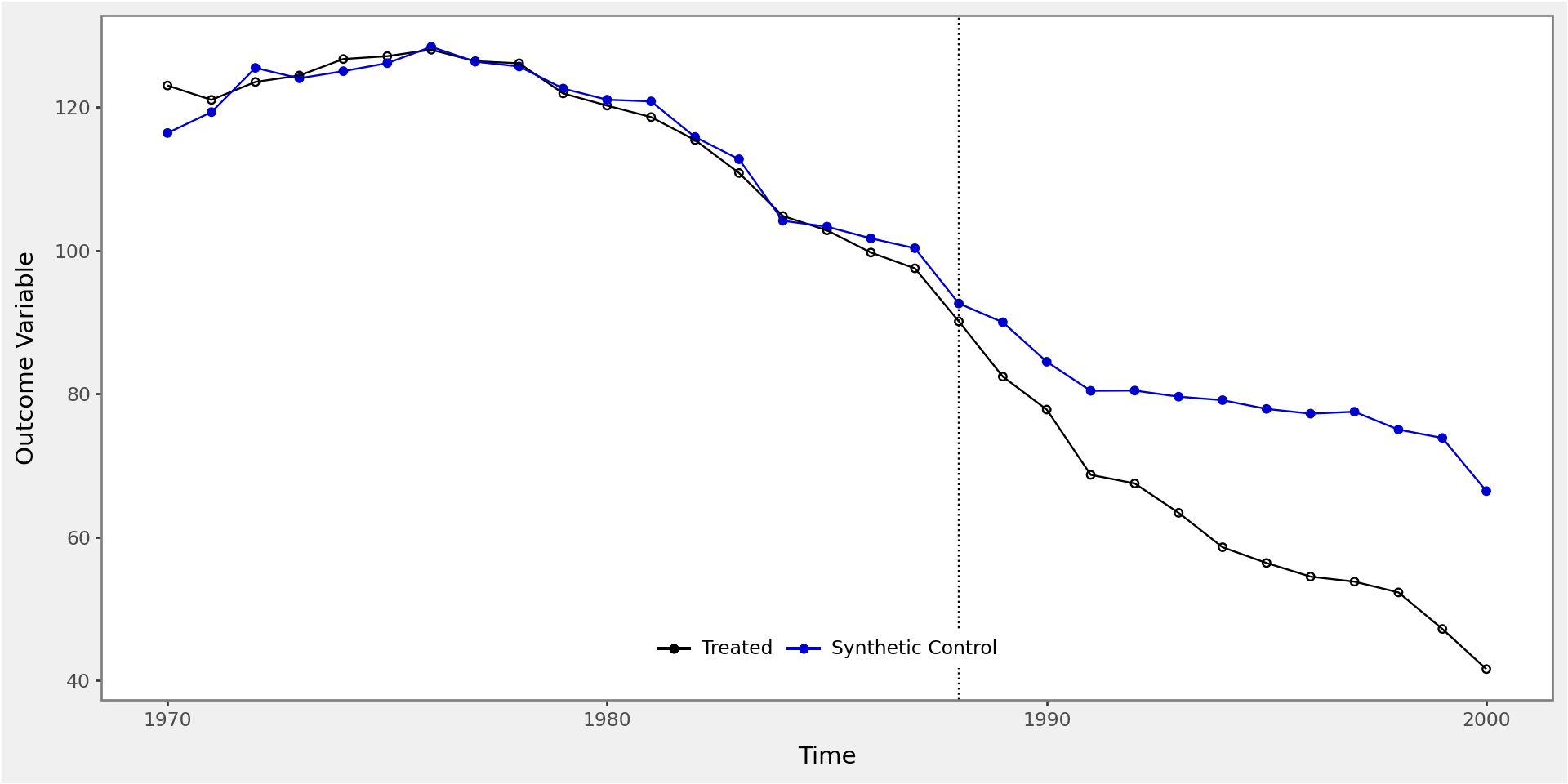
calif_synth = cigar.query("~california").pivot(index='year', columns="state")["cigsale"].values.dot(calif_weights)
plt.figure(figsize=(10,6))
plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"], label="California")
plt.plot(cigar.query("california")["year"], calif_synth, label="Synthetic Control")
plt.vlines(x=1988, ymin=40, ymax=140, linestyle=":", lw=2, label="Proposition 99")
plt.ylabel("Per-capita cigarette sales (in packs)")
plt.legend()
plt.show()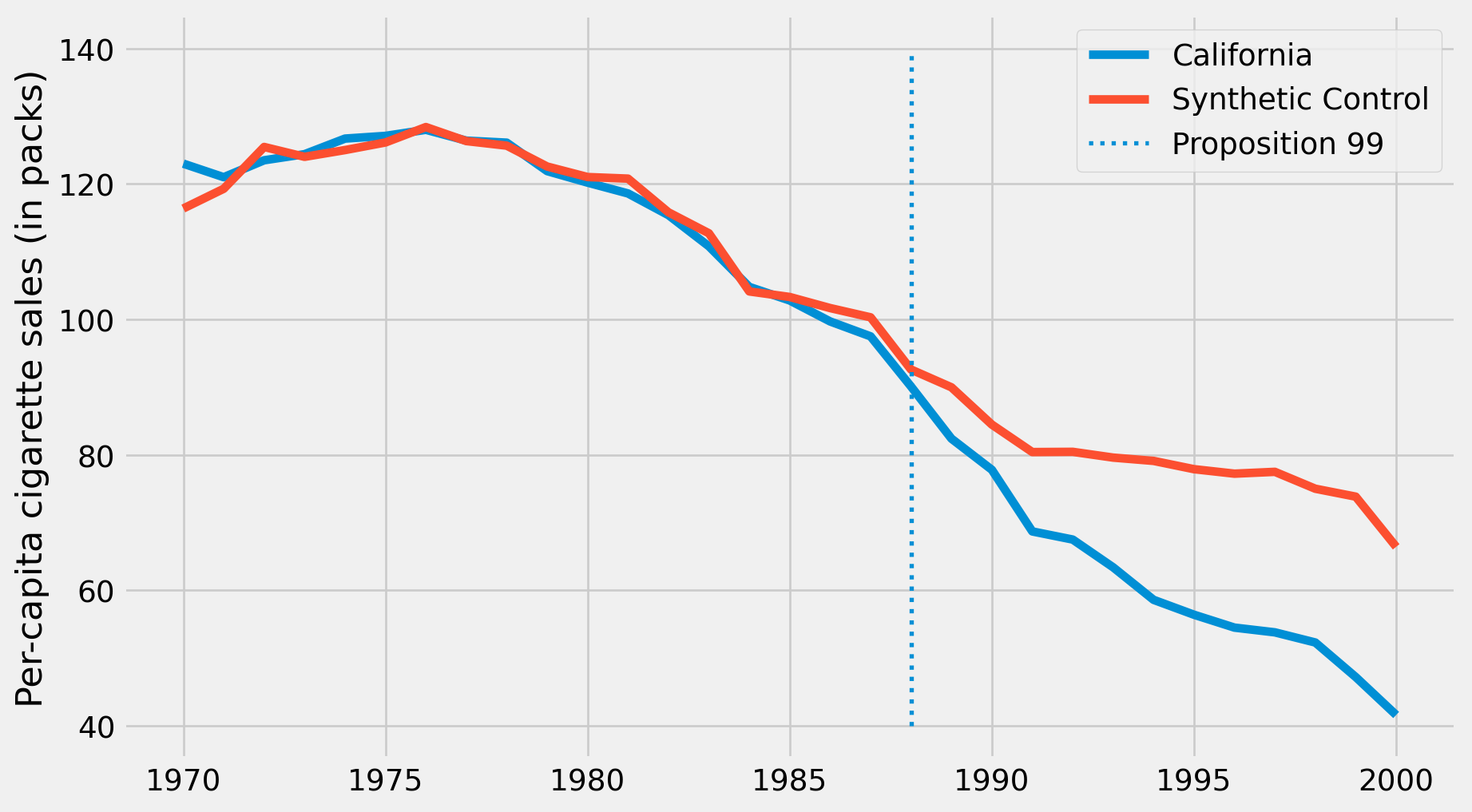

When Does this Work?

  • If data generated by linear factor model: \[ Y_{jt}(0) = \delta_t + \theta_t Z_j + \lambda_t \mu_j + \epsilon_{jt} \]
    • Observed \(Z_j\)
    • Unobserved\(\lambda_t\), \(\mu_j\)
  • As \(T_0\) increases or variance of \(\epsilon_{jt}\) decreases, bias of \(\hat{\tau}_{it}\) decreases
    • Needs \(\mathbf{X}_1 \approx \mathbf{X}_0 W\)

Choices

  • Variables in \(\mathbf{X}\) to match
    • Fewer make eaiser to have \(\mathbf{X}_1 \approx \mathbf{X}_0 W\)
    • But fewer make \(W\) depend more on \(\epsilon\)
  • Set of untreated units to consider
    • More units makes eaiser to have \(\mathbf{X}_1 \approx \mathbf{X}_0 W\)
    • But risk of overfitting

Inference

Inference

  • Estimator \[ \hat{\tau}_{1t} = Y_{1t} - \underbrace{\sum_{j=2}^{J+1} \hat{w}_j Y_{jt}}_{\hat{Y}_{1t}(0)} \]
    • single observation of \(Y_{1t}\)
    • \(\hat{w}_j\) depends on pre-treatment variables \(\underbrace{\mathbf{X}_1, \mathbf{X}_0}_{(J+1) \times (T_0 + K)}\)
    • \(J\) values of \(Y_{jt}\)
  • Usual asymptotics not applicable

Treatment Permutation

  • Compute estimate pretending each of the \(J\) untreated units were treated instead
  • Use as distribution of \(\hat{\tau}_{1t}\) under \(H_0: \tau_{1t} = 0\)

Treatment Permutation

def synthetic_control(state: int, data: pd.DataFrame) -> np.array:
    features = ["cigsale", "retprice"]
    inverted = (data.query("~after_treatment")
                .pivot(index='state', columns="year")[features]
                .T)
    X1 = inverted[state].values # treated
    X0 = inverted.drop(columns=state).values # donor pool

    weights = get_w(X0, X1)
    synthetic = (data.query(f"~(state=={state})")
                 .pivot(index='year', columns="state")["cigsale"]
                 .values.dot(weights))
    return (data
            .query(f"state=={state}")[["state", "year", "cigsale", "after_treatment"]]
            .assign(synthetic=synthetic))

from joblib import Parallel, delayed

control_pool = cigar["state"].unique()
parallel_fn = delayed(partial(synthetic_control, data=cigar))
synthetic_states = Parallel(n_jobs=20)(parallel_fn(state) for state in control_pool);

Treatment Permutation

Code 
plt.figure(figsize=(12,7))
for state in synthetic_states:
    plt.plot(state["year"], state["cigsale"] - state["synthetic"], color="C5",alpha=0.4)

plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"] - calif_synth,
        label="California");

plt.vlines(x=1988, ymin=-50, ymax=120, linestyle=":", lw=2, label="Proposition 99")
plt.hlines(y=0, xmin=1970, xmax=2000, lw=3)
plt.ylabel("Gap in per-capita cigarette sales (in packs)")
plt.title("State - Synthetic Across Time")
plt.legend()
plt.show()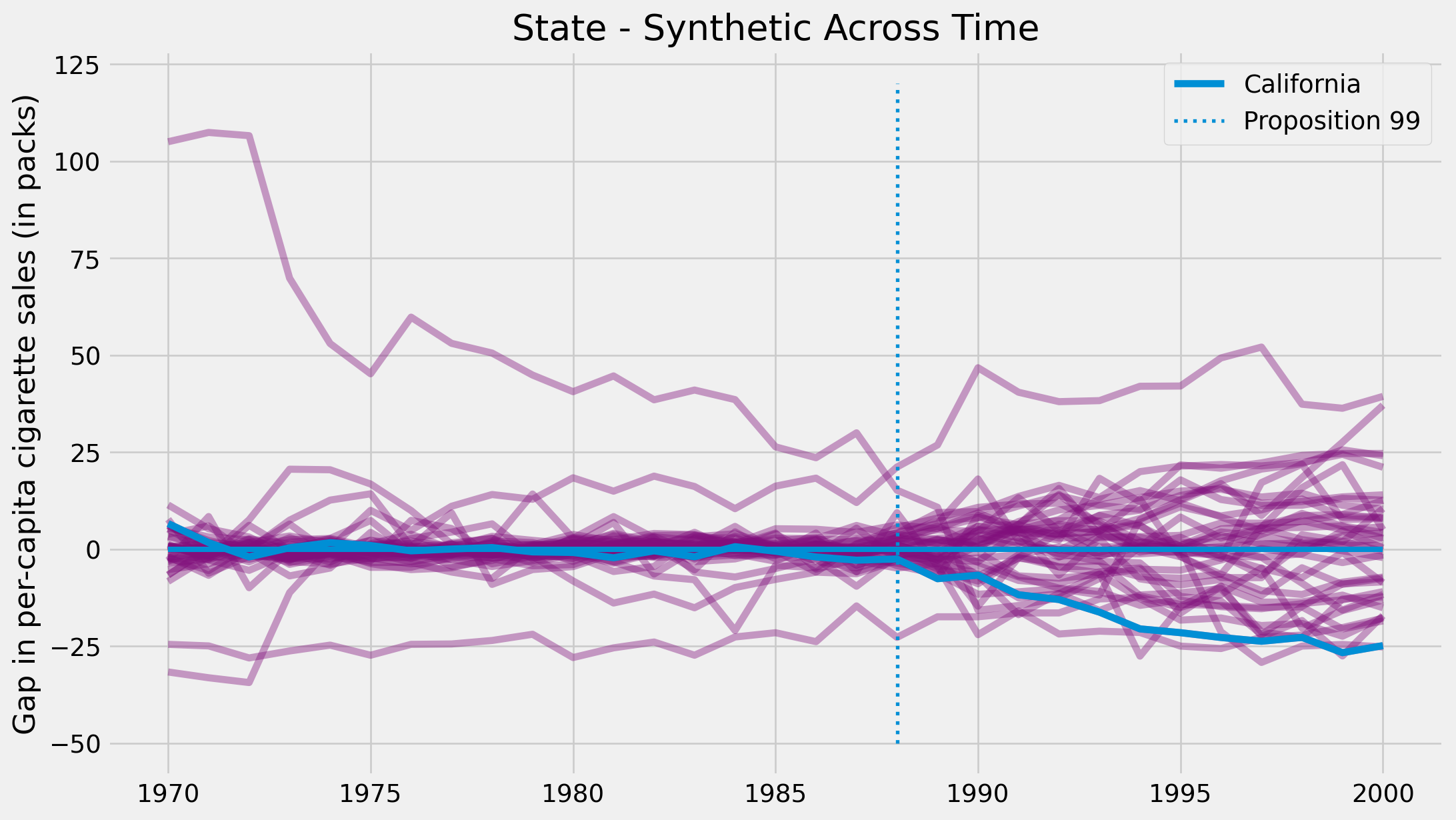

Treatment Permutation Inference

Code 
def pre_treatment_error(state):
    pre_treat_error = (state.query("~after_treatment")["cigsale"]
                       - state.query("~after_treatment")["synthetic"]) ** 2
    return pre_treat_error.mean()

plt.figure(figsize=(12,7))
for state in synthetic_states:

    # remove units with mean error above 80.
    if pre_treatment_error(state) < 80:
        plt.plot(state["year"], state["cigsale"] - state["synthetic"], color="C5",alpha=0.4)

plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"] - calif_synth,
        label="California");

plt.vlines(x=1988, ymin=-50, ymax=120, linestyle=":", lw=2, label="Proposition 99")
plt.hlines(y=0, xmin=1970, xmax=2000, lw=3)
plt.ylabel("Gap in per-capita cigarette sales (in packs)")
plt.title("Distribution of Effects")
plt.title("State - Synthetic Across Time (Large Pre-Treatment Errors Removed)")
plt.legend()
plt.show()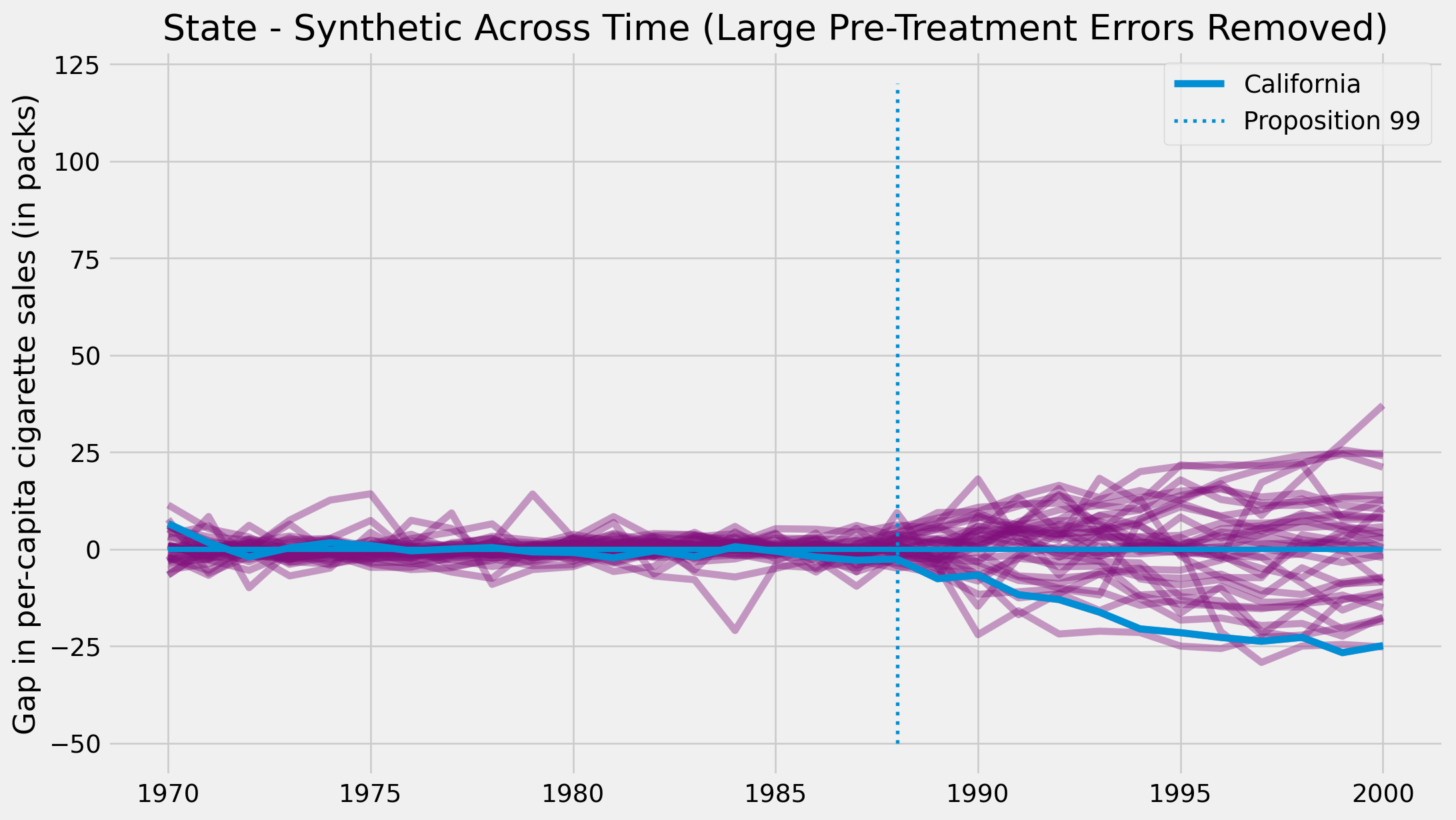

Treatment Permutation Inference: Testing \(H_0: \tau=0\)

calif_number = 3

effects = [state.query("year==2000").iloc[0]["cigsale"] - state.query("year==2000").iloc[0]["synthetic"]
           for state in synthetic_states
           if pre_treatment_error(state) < 80] # filter out noise

calif_effect = cigar.query("california & year==2000").iloc[0]["cigsale"] - calif_synth[-1]

print("California Treatment Effect for the Year 2000:", calif_effect)

np.mean(np.array(effects) < calif_effect)
California Treatment Effect for the Year 2000: -24.83015975607075
np.float64(0.02857142857142857)

Design Based Inference

  • Sampling based inference:
    • Specify data generating process (DGP)
    • Find distribution of estimator under repeated sampling of datasets from DGP
  • Design based inference:
    • Condition on dataset you have
    • Randomness of estimator from random assignment of treatment
    • See Abadie et al. (2020) for more information
  • Treatment permutation inference is design based inference assuming the treated unit was chosen uniformly at random from all units

Design Based / Treatment Permutation Inference

  • Pros:
    • Easy to implement and explain
    • Intuitive appeal, similar to placebo tests
    • Minimal assumptions about DGP
  • Cons:
    • Assumption about randomized treatment assignment is generally false
    • Needs modification to test hypotheses other than \(H_0: \tau=0\) & to construct confidence intervals

Prediction Intervals

  • Estimation error is a prediction error \[ \begin{align*} \hat{\tau}_{1t} = & Y_{1t} - \underbrace{\hat{Y}_{1t}(0)}_{\text{prediction given $Y_{jt}, \mathbf{X}_0$}} \\ = & \underbrace{Y_{1t}(1) - \color{grey}{Y_{1t}(0)}}_{\tau_{1t}} + \underbrace{\color{grey}{Y_{1t}(0)} - \hat{Y}_{1t}(0)}_{\text{prediction error}} \end{align*} \]
  • Many statistical methods for calculating distribution of prediction error
  • Difficulties:
    • High-dimensional: number of weights comparable to number of observations and dimension of predictors
    • Moderate sample sizes

Prediction Intervals

  • Modern approaches accomodate high-dimensionality and give non-asymptotic results
  • Chernozhukov, Wüthrich, and Zhu (2021) : construct prediction intervals by permuting residuals (conformal inference)
  • Cattaneo, Feng, and Titiunik (2021) : divide prediction error into two pieces: estimation of \(\hat{w}\) and unpredictable randomness in \(Y_{1t}(0)\)

Catteneo, Feng, & Titiunik

  • Given coverage level \(\alpha\), gives interval \(\mathcal{I}_{1-\alpha}\) such that \[ P\left[ P\left(\tau_{1t} \in \mathcal{I}_{1-\alpha} | \mathbf{X}_0, \{y_{jt}\}_{j=1}^J\right) > 1-\alpha-\epsilon(T_0) \right] > 1 - \pi(T_0) \] where \(\epsilon(T_0) \to 0\) and \(\pi(T_0) \to 0\) as \(T_0 \to \infty\)

  • prediction error comes from

    1. estimation of \(\hat{w}\), options refer to u_ in scpi_pkg
    2. unobservable stochastic error in \(Y_{1t}(0)\), options begin with e_ in scpi_pkg

  • valid under broad range of DGPs, but appropriate interval does depend on dependence of data over time, stationarity, assumptions about distribution of error given predictors

Software

  • scpi_pkg recommended, created by leading econometricians
  • pysyncon actively maintained, well-documented, but appears not popular
  • SpareSC created by researchers at Microsoft, uses particular variant
  • scinference R package accompanying Chernozhukov, Wüthrich, and Zhu (2021)

scpi_pkg

Data Preparation

import random
from scpi_pkg.scdata import scdata
from scpi_pkg.scest import scest
from scpi_pkg.scplot import scplot
scdf = scdata(df=cigar, id_var="state", time_var="year", outcome_var="cigsale",
              period_pre=cigar.query("not after_treatment").year.unique(),
              period_post=cigar.query("after_treatment").year.unique(),
              unit_tr=calif_number,
              unit_co=cigar.query("not california").state.unique(),
              features=["cigsale","retprice"],
              cov_adj=None, cointegrated_data=True,
              constant=False)

Point Estimation

Code 
est_si = scest(scdf, w_constr={'name': "simplex"})
print(est_si)
est_si2 = scest(scdf, w_constr={'p': 'L1', 'dir': '==', 'Q': 1, 'lb': 0})
print(est_si2)
scplot(est_si)
-----------------------------------------------------------------------
Call: scest
Synthetic Control Estimation - Setup

Constraint Type:                                                simplex
Constraint Size (Q):                                                  1
Treated Unit:                                                         3
Size of the donor pool:                                              38
Features                                                              2
Pre-treatment period                                          1970-1988
Pre-treatment periods used in estimation per feature:
 Feature  Observations
 cigsale            19
retprice            19
Covariates used for adjustment per feature:
 Feature  Num of Covariates
 cigsale                  0
retprice                  0

Synthetic Control Estimation - Results

Active donors: 5

Coefficients:
                    Weights
Treated Unit Donor         
3            1        0.000
             10       0.000
             11       0.000
             12       0.000
             13       0.000
             14       0.000
             15       0.000
             16       0.000
             17       0.000
             18       0.000
             19       0.000
             2        0.000
             20       0.000
             21       0.113
             22       0.105
             23       0.457
             24       0.000
             25       0.000
             26       0.000
             27       0.000
             28       0.000
             29       0.000
             30       0.000
             31       0.000
             32       0.000
             33       0.000
             34       0.240
             35       0.000
             36       0.000
             37       0.000
             38       0.000
             39       0.000
             4        0.000
             5        0.085
             6        0.000
             7        0.000
             8        0.000
             9        0.000

-----------------------------------------------------------------------
Call: scest
Synthetic Control Estimation - Setup

Constraint Type:                                          user provided
Constraint Size (Q):                                                  1
Treated Unit:                                                         3
Size of the donor pool:                                              38
Features                                                              2
Pre-treatment period                                          1970-1988
Pre-treatment periods used in estimation per feature:
 Feature  Observations
 cigsale            19
retprice            19
Covariates used for adjustment per feature:
 Feature  Num of Covariates
 cigsale                  0
retprice                  0

Synthetic Control Estimation - Results

Active donors: 5

Coefficients:
                    Weights
Treated Unit Donor         
3            1        0.000
             10       0.000
             11       0.000
             12       0.000
             13       0.000
             14       0.000
             15       0.000
             16       0.000
             17       0.000
             18       0.000
             19       0.000
             2        0.000
             20       0.000
             21       0.113
             22       0.105
             23       0.457
             24       0.000
             25       0.000
             26       0.000
             27       0.000
             28       0.000
             29       0.000
             30       0.000
             31       0.000
             32       0.000
             33       0.000
             34       0.240
             35       0.000
             36       0.000
             37       0.000
             38       0.000
             39       0.000
             4        0.000
             5        0.085
             6        0.000
             7        0.000
             8        0.000
             9        0.000

Inference

Code 
from scpi_pkg.scpi import scpi
import random
w_constr = {'name': 'simplex', 'Q': 1}
u_missp = True
u_sigma = "HC1"
u_order = 1
u_lags = 0
e_method = "gaussian"
e_order = 1
e_lags = 0
e_alpha = 0.05
u_alpha = 0.05
sims = 200
cores = 1

random.seed(8894)
result = scpi(scdf, sims=sims, w_constr=w_constr, u_order=u_order, u_lags=u_lags,
              e_order=e_order, e_lags=e_lags, e_method=e_method, u_missp=u_missp,
              u_sigma=u_sigma, cores=cores, e_alpha=e_alpha, u_alpha=u_alpha)
scplot(result, e_out=True, x_lab="year", y_lab="per-capita cigarette sales (in packs)")
-----------------------------------------------
Estimating Weights...
Quantifying Uncertainty

20/200 iterations completed (10%)
40/200 iterations completed (20%)
60/200 iterations completed (30%)
80/200 iterations completed (40%)
100/200 iterations completed (50%)
120/200 iterations completed (60%)
140/200 iterations completed (70%)
160/200 iterations completed (80%)
180/200 iterations completed (90%)
200/200 iterations completed (100%)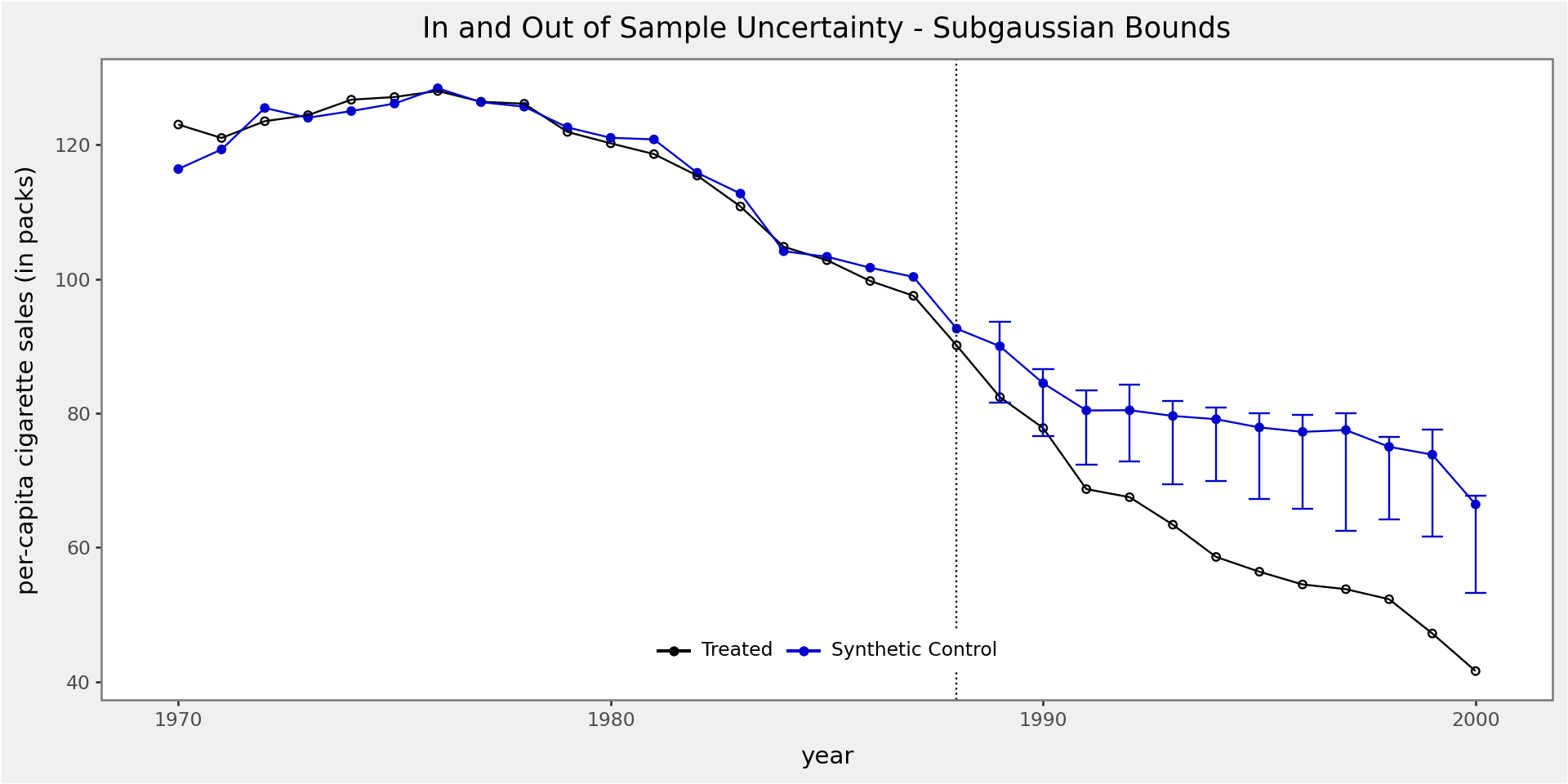

Sources and Further Reading

  • example code from Facure (2022) chapter 15
  • notation and theory follows Abadie (2021)
  • Huntington-Klein (2021) chapter 21.2
  • More technical:
    • Cattaneo et al. (2022) user guide for scpi_pkg
    • Abadie, Diamond, and Hainmueller (2010) important paper popularizing synthetic control and permutation inference
    • Abadie and Cattaneo (2021) lists recent statistical advances in synthetic control

References

Abadie, Alberto. 2021. “Using Synthetic Controls: Feasibility, Data Requirements, and Methodological Aspects.” Journal of Economic Literature 59 (2): 391–425. https://doi.org/10.1257/jel.20191450.
Abadie, Alberto, Susan Athey, Guido W. Imbens, and Jeffrey M. Wooldridge. 2020. “Sampling-Based Versus Design-Based Uncertainty in Regression Analysis.” Econometrica 88 (1): 265–96. https://doi.org/https://doi.org/10.3982/ECTA12675.
Abadie, Alberto, and Matias D. Cattaneo. 2021. “Introduction to the Special Section on Synthetic Control Methods.” Journal of the American Statistical Association 116 (536): 1713–15. https://doi.org/10.1080/01621459.2021.2002600.
Abadie, Alberto, Alexis Diamond, and Jens Hainmueller. 2010. “Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program.” Journal of the American Statistical Association 105 (490): 493–505. https://doi.org/10.1198/jasa.2009.ap08746.
Cattaneo, Matias D., Yingjie Feng, Filippo Palomba, and Rocio Titiunik. 2022. “Scpi: Uncertainty Quantification for Synthetic Control Methods.”
Cattaneo, Matias D., Yingjie Feng, and Rocio Titiunik. 2021. “Prediction Intervals for Synthetic Control Methods.” Journal of the American Statistical Association 116 (536): 1865–80. https://doi.org/10.1080/01621459.2021.1979561.
Chernozhukov, Victor, Kaspar Wüthrich, and Yinchu Zhu. 2021. “An Exact and Robust Conformal Inference Method for Counterfactual and Synthetic Controls.” Journal of the American Statistical Association 116 (536): 1849–64. https://doi.org/10.1080/01621459.2021.1920957.
Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.
Huntington-Klein, Nick. 2021. The Effect: An Introduction to Research Design and Causality. CRC Press. https://theeffectbook.net/.