ECON622: Computational Economics with Data Science Applications

Transformers and Attention

Jesse Perla
jesse.perla@ubc.ca

University of British Columbia

Overview

Summary

  • Describe “attention” with function approximation and relate to kernels and similarity
  • Describe transformers, the architecture that which makes LLMs possible
  • Give intuition on how/when transformers can work
  • Describe it more generally as a tool for sequential and set-based data (e.g., graphs, images)

References

Attention

Reminder: Kernel Regression

  • Recall in the Kernels/GP lecture we discussed how we can define a kernel to do pairwise comparisons of two inputs form a set of data \(X = \{x_1, x_2, \ldots, x_n\}\) with outputs \(Y = \{y_1, y_2, \ldots, y_n\}\).
    • \(\mathcal{K}(x_i, x_j)\) is a measure of similarity between \(x_i\) and \(x_j\).
    • Then, for a new \(x\), we could define a vector of similarity scores, \(\alpha \equiv [\mathcal{K}(x, x_i)]_{i=1}^N\)
    • And “predict” a \(y(x)\) as a weighted sum of the \(y_i\)’s \[ y(x) \approx \sum_{i=1}^n \mathcal{K}(x, x_i) y_i = \alpha \cdot Y \]
  • Non-parametric, with potentially infinite-dimensional feature spaces

Look-up Tables

  • We can think of a Kernel regression as a non-parametric model of attention (see ProbML Book 1 15.4.2)
  • A crude way to think of this is as a fuzzy look-up table
    1. Take a query, \(x\), and look keys, \(x_i\), which are similar. Score by \(\alpha_i\)
      • The score of similarity is a dot-product of the query \(x\) and the key \(x_i\)
      • Normalize to probability,so \(\sum \alpha_i = 1\)
    2. Then with a value \(y_i\) associated with each key, we can get an average value of the \(y_i\)’s weighted by the \(\alpha_i\)’s

Parametric Version

  • Taking that inspiration, we want to define a version of this which is parametric (i.e., it will not require saving all the data in memory) and is differentiable
    • To be parametric, replace the fixed kernels based on the data with a parametric form as a learned embedding
    • In order to be differentiable, we want to replace a fixed lookup table with a probabilistic one
  • Kernel Regressions evaluated on new \(\{x_1, \ldots x_n\}\) required pairwise comparison within that set, and across all previous data.
    • Parametric versions can just compare the new \(x\) to each other pairwise using the embedding
  • See ProbML Book 1 Section 15.4 and ProbML Book 2 Section 16.2.7 for more

Mapping to an Embedding Space

  • First, lets separate out query and key to be more general
  • Map the inputs, \(x\in\mathbb{R}^h\), with a linear embedding into \(d\) dimensional space
    • \(q = W_Q x\) for \(W_Q \in \mathbb{R}^{d \times h}\)
  • Map each of \(m\) keys into a similar \(d\) dimensional space (keys and queries can be different)
    • \(k = W_K x\) for \(W_K \in \mathbb{R}^{d \times h}\)
    • Depending on circumstances, possibly \(y = W_Y x\) for \(W_Y \in \mathbb{R}^{v \times h}\)
  • Associate a \(v\) dimensional value with each key
  • Stack up the \(K \in \mathbb{R}^{m \times d}\) and \(V \in \mathbb{R}^{m \times v}\)

Attention for a Single “Query”

  • Given a \(q\), the attention is \[ \begin{aligned} \text{Attn}(q, K, V) &\equiv \sum_{i=1}^m \alpha_i(q, K)\cdot V_i\\ \alpha_i(q, K) &\equiv \frac{\exp(a(q, K_i))}{\sum_{j=1}^m \exp(a(q, K_j))}\\ a(q, k) &\equiv q \cdot k/\sqrt{d} \end{aligned} \]
  • Returns the value weighted by probabilities (i.e., a softmax of the similarity between the query and each key)
  • Dot-product similarity, rescaling by \(\sqrt{d}\) is to normalize

Interpretation

A standard, broad interpretation attention for tokens

  • The query contains what information a token is looking for
  • The key contains what type of information a token provides
  • The value contains what information is returned

Attention Layer

  • Typically we are calculating the attention for \(n\) batches of the embedded inputs
  • Use \(W_Q\) to embed inputs, \(Q \in \mathbb{R}^{n \times d}\), then \[ Z = \text{Attn}(Q, K, V) = \text{softmax}\left(\frac{Q K^{\top}}{\sqrt{d}}\right)V \in \mathbb{R}^{n \times v} \]
    • The parameters to “learn” are just the embeddings, \(W_Q, W_K\) and potentially \(W_V\)

Self-Attention

  • If the \(Q, K,\) and \(V\) come from the same data, then it is called self-attention
    • Canonical example might be that \(X\) are an embedded tokens of a sentence
  • That is, if we have a \(X\in\mathbb{R}^{h\times n}\) which are basic embeddings of the tokens and set \(Q = W_Q X, K = W_K X, V = W_V X\), \[ Z = \text{Attn}(W_Q X, W_K X, W_V X) \in \mathbb{R}^{n \times v} \]
    • Note that this makes pairwise comparisons for all \(n\)

Multi-Head Attention

  • There will be different senses of similarity for the query, key, and value.

  • A powerful approach is to to have multiple self-attention layers \(j=1,\ldots J\) \[ Z^j = \text{Attn}(W_Q^j X, W_K^j X, W_V^j X) \]

  • Then concatenate the \(Z^j\)’s and potentially project with embedding \(W_O\)

    \[ {\small \text{MultiHead}(X) = W_O\cdot \begin{bmatrix}\text{Attn}(W_Q^1 X, W_K^1 X, W_V^1 X)\\ \vdots\\\text{Attn}(W_Q^J X, W_K^J X, W_V^J X)\end{bmatrix} } \]

    • “Trainable” parameters are the \(W_Q^j, W_K^j, W_V^j, W_O\)

Invariant to Ordering? Add Position

  • In this simple example, the tokens are all treated as pointwise comparisons without any sense of “ordering”
    • i.e., invariant to permutations of \(X\). For some tasks, that is appropriate
    • For others, the order of the tokens in a “sentence” is crucial.
  • Solution: embedding tokens, \(X\), combined with its position
    • While one could think of jointly embedding the token with an integer index, that is not differentiable
    • Instead, tricks such as mapping the position to a vector through sinusoidal functions. See Attention is All You Need
  • The word embedding and the position embedding are combined before the first Multi-Head Attention layer

Attention Visualization of \(\alpha\)

  • Attention lets one point of the input be strongly influenced by others in a context-dependent way
  • See the above, which associates the word “it” with “animal” when the pronoun needs to be interpreted in context

Token Prediction

  • Recall with the ChatGPT style prediction of the next token, we need to find a \(\mathbb{P}(x_t | x_{t-1}, x_{t-2}, \ldots, x_1)\)
    • Where the \(t\) might be \(128k\) or more, and there might be \(50K\) possible discrete \(x_t\) states
  • Attention is central because it can find representations of the \(x_{t-1}, x_{t-2}, \ldots, x_1\) for conditioning
    • Self-attention makes it possible for the representations to capture the features of the joint distribution of previous tokens

Transformers

A Marvel of Modern Engineering

  • The transformer architecture is a highly efficient, numerically stable, parallelizable, and regularized way to use attention
  • Transformers are built using:
    • One or more Multi-head self-attention layers
    • Flexible NN approximations (feed forward in diagram) to map the MHA output to a nonlinear functions
    • Positional encoding tricks to encode ordering of data
    • Softmax (i.e., logit) to map high-dimensional latent spaces to probabilities
    • Various tricks (LayerNorm, Dropout) , etc. to make the model more numerically stable and regularized
    • “Masking” and other ways to enable self-supervised learning and various tasks, and ensure training is done token-by-token

Example Encoder-Decoder Transformer Architecture

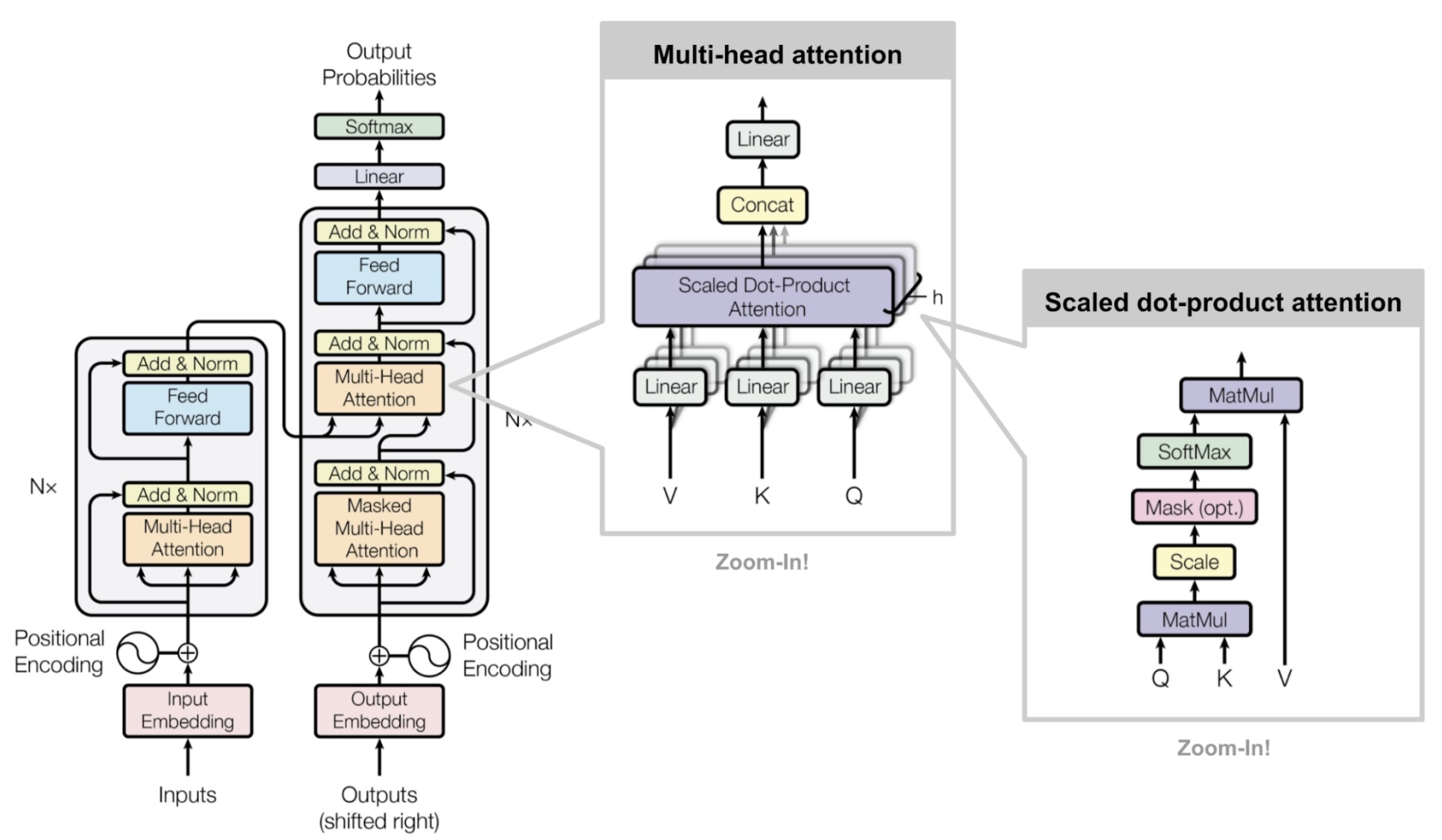
Sequence to Sequence

  • Early transformer designed for translation tasks (sequence of tokens as input to sequence of tokens as output)
    • i.e., the \(\mathbb{P}(y_1, \ldots y_T|x_1, \ldots x_T)\) where \(T\) might be enormous, and \(x,y\) might allow tens of thousands of tokens
  • The design of these typically uses a transformer to encode \(x_1,\ldots x_T\) into a representation, then another to decode, and take the representation back to the \(y_1, \ldots y_T\) tokens

Decoder-Only Transformer

  • To generate text token by token, as in the Sequential Generation can use a single transformer
    • i.e., the \(\mathbb{P}(x_{T+1}|x_1, \ldots x_T)\)
  • This embeds the previous tokens, \(x_1, \ldots x_T\) to generate a PMF over the next one.
  • Decoder-only because a single transformer is used the end-result is the token output probabilities

Encoder-Only Transformer

  • For tasks like classification, the transformer can be be used to simply encode an internal representation of the input for a downstream task like classification
    • i.e., the \(\mathbb{P}(\text{Class}(x_1, \ldots x_T) = C_i |x_1, \ldots x_T)\)
  • Then the final layer can be used to classify the input using standard techniques
  • This is called an Encoder-Only transformer because the end-result is the internal representation

Not Just for Text

  • The basic idea of attention is useful whenever there are parts of the data where the representations work best if parts of the data are compared to other parts
  • For example, can use transformers with images
    • For those, the “position” might be patches of the image
  • Another example are working with graphs/networks
    • For that, the “position” might help you to find distances between nodes in the graph