Difference in Differences II
ECON526
Paul Schrimpf
University of British Columbia
Difference in Differences
\[ \def\Er{{\mathrm{E}}} \def\En{{\mathbb{E}_n}} \def\cov{{\mathrm{Cov}}} \def\var{{\mathrm{Var}}} \def\R{{\mathbb{R}}} \newcommand\norm[1]{\left\lVert#1\right\rVert} \def\rank{{\mathrm{rank}}} \newcommand{\inpr}{ \overset{p^*_{\scriptscriptstyle n}}{\longrightarrow}} \def\inprob{{\,{\buildrel p \over \rightarrow}\,}} \def\indist{\,{\buildrel d \over \rightarrow}\,} \DeclareMathOperator*{\plim}{plim} \]
Setup
TwoMany periods, binary treatment insecondsome periods- Potential outcomes \(\{y_{it}(0),y_{it}(1)\}_{t=1}^T\) for \(i=1,...,N\)
- Treatment \(D_{it} \in \{0,1\}\),
- \(D_{i0} = 0\) \(\forall i\)
- \(D_{i1} = 1\) for some, \(0\) for others
- Observe \(y_{it} = y_{it}(0)(1-D_{it}) + D_{it} y_{it}(1)\)
Identification
Same logic as before, \[ \begin{align*} ATT_{t,t-s} & = \Er[y_{it}(1) - \color{red}{y_{it}(0)} | D_{it} = 1, D_{it-s}=0] \\ & = \Er[y_{it}(1) - y_{it-s}(0) | D_{it} = 1, D_{it-s}=0] - \\ & \;\; - \Er[\color{red}{y_{it}(0)} - y_{t-s}(0) | D_{it}=1, D_{it-s}=0] \end{align*} \]
- assume \(\Er[\color{red}{y_{it}(0)} - y_{it-s}(0) | D_{it}=1, D_{it-s}=0] = \Er[y_{it}(0) - y_{it-s}(0) | D_{it}=0, D_{it-s}=0]\)
\[ \begin{align*} ATT_{t,t-s}& = \Er[y_{it} - y_{it-s} | D_{it}=1, D_{it-s}=0] - \Er[y_{it} - y_{it-s} | D_{it}=0, D_{it-s}=0] \end{align*} \] - Similarly, can identify various other interpretable average treatment effects conditional on being treated at some times and not others
Estimation
Plugin
Fixed effects? \[ y_{it} = \beta D_{it} + \alpha_i + \delta_t + \epsilon_{it} \] When will \(\hat{\beta}^{FE}\) consistently estimate some interpretable conditional average of treatment effects?
Fixed Effects
- As with matching, \[ \begin{align*} \hat{\beta} = & \sum_{i=1,t=1}^{n,T} y_{it} \overbrace{\frac{\tilde{D}_{it}}{ \sum_{i,t} \tilde{D}_{it}^2 }}^{\hat{\omega}_{it}} = \sum_{i=1,t=1}^{n,T} y_{it}(0) \hat{\omega}_{it} + \sum_{i=1,t=1}^{n,T} D_{it} (y_{it}(1) - y_{it}(0)) \hat{\omega}_{it} \end{align*} \] where \[ \begin{align*} \tilde{D}_{it} & = D_{it} - \frac{1}{n} \sum_{j=1}^n (D_{jt} - \frac{1}{T} \sum_{s=1}^T D_{js}) - \frac{1}{T} \sum_{s=1}^T D_{is} \\ & = D_{it} - \frac{1}{n} \sum_{j=1}^n D_{jt} - \frac{1}{T} \sum_{s=1}^T D_{is} + \frac{1}{nT} \sum_{j,s} D_{js} \end{align*} \]
Weights
def assigntreat(n, T, portiontreated):
treated = np.zeros((n, T), dtype=bool)
for t in range(1, T):
treated[:, t] = treated[:, t - 1]
if portiontreated[t] > 0:
treated[:, t] = np.logical_or(treated[:, t-1], np.random.rand(n) < portiontreated[t])
return treated
def weights(D):
D̈ = D - np.mean(D, axis=0) - np.mean(D, axis=1)[:, np.newaxis] + np.mean(D)
ω = D̈ / np.sum(D̈**2)
return ω
n = 100
T = 9
pt = np.zeros(T)
pt[T//2 + 1] = 0.5
D = assigntreat(n, T,pt)
y = np.random.randn(n, T)
weighted_sum = np.sum(y * weights(D))
print(weighted_sum)-0.06058394152339747Using a package
###
Estimation: OLS
Dep. var.: y, Fixed effects: id + t
sample: None = all
Inference: CRV1
Observations: 900
| Coefficient | Estimate | Std. Error | t value | Pr(>|t|) | 2.5% | 97.5% |
|:--------------|-----------:|-------------:|----------:|-----------:|-------:|--------:|
| D | -0.061 | 0.125 | -0.487 | 0.628 | -0.308 | 0.186 |
---
RMSE: 0.966 R2: 0.128 R2 Within: 0.0 Weights with Single Treatment Time
Code
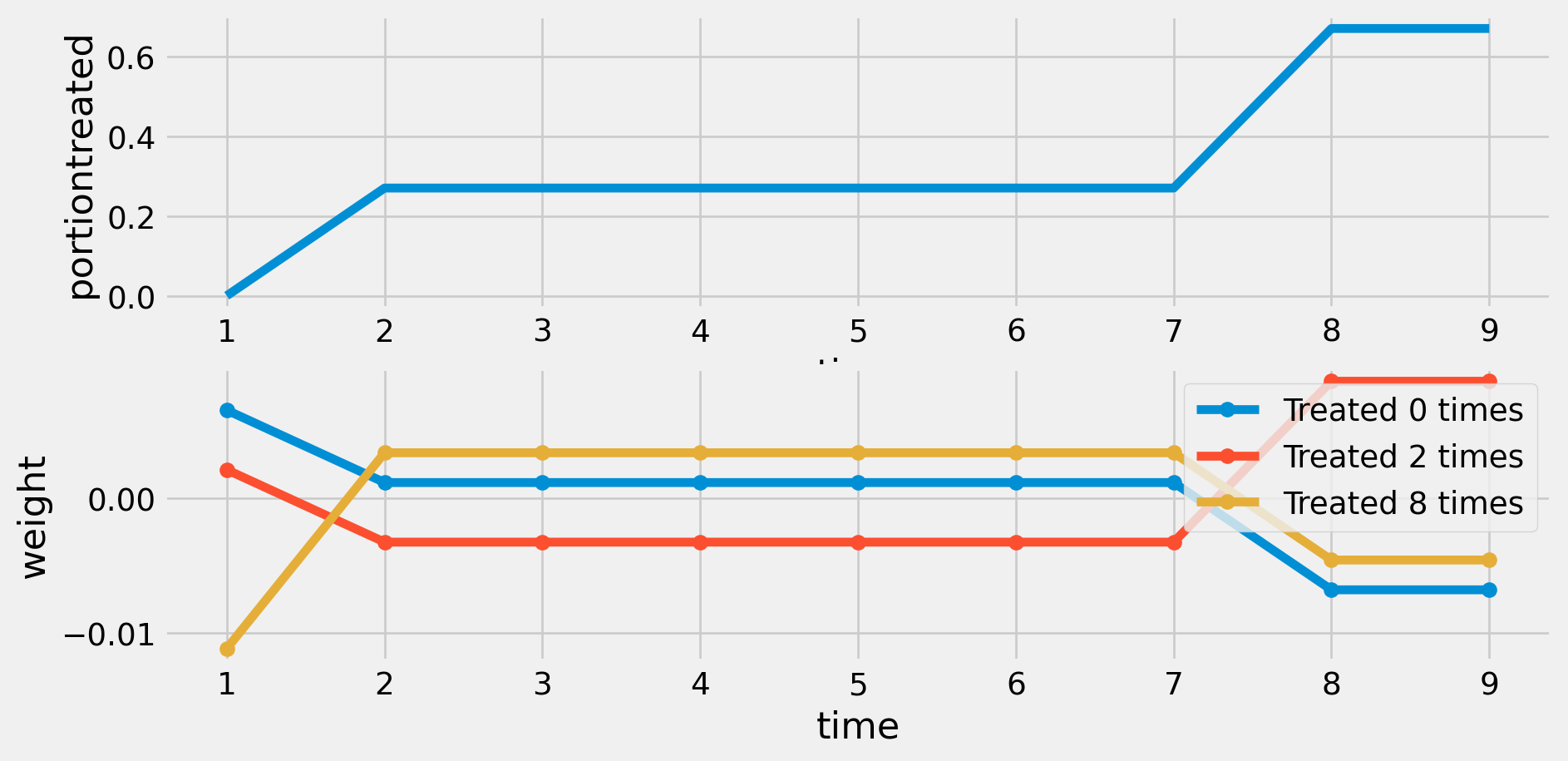
def plotD(D,ax):
n, T = D.shape
ax.set(xlabel='time',ylabel='portiontreated')
ax.plot(range(1,T+1),D.mean(axis=0))
ax
def plotweights(D, ax):
n, T = D.shape
ω = weights(D)
groups = np.unique(D, axis=0)
ax.set(xlabel='time', ylabel='weight')
for g in groups:
i = np.where(np.all(D == g, axis=1))[0][0]
wt = ω[i, :]
ax.plot(range(1, T+1), wt, marker='o', label=f'Treated {np.sum(g)} times')
ax.legend()
ax
def plotwd(D):
fig, ax = plt.subplots(2,1)
ax[0]=plotD(D,ax[0])
ax[1]=plotweights(D,ax[1])
plt.show()
plotwd(D)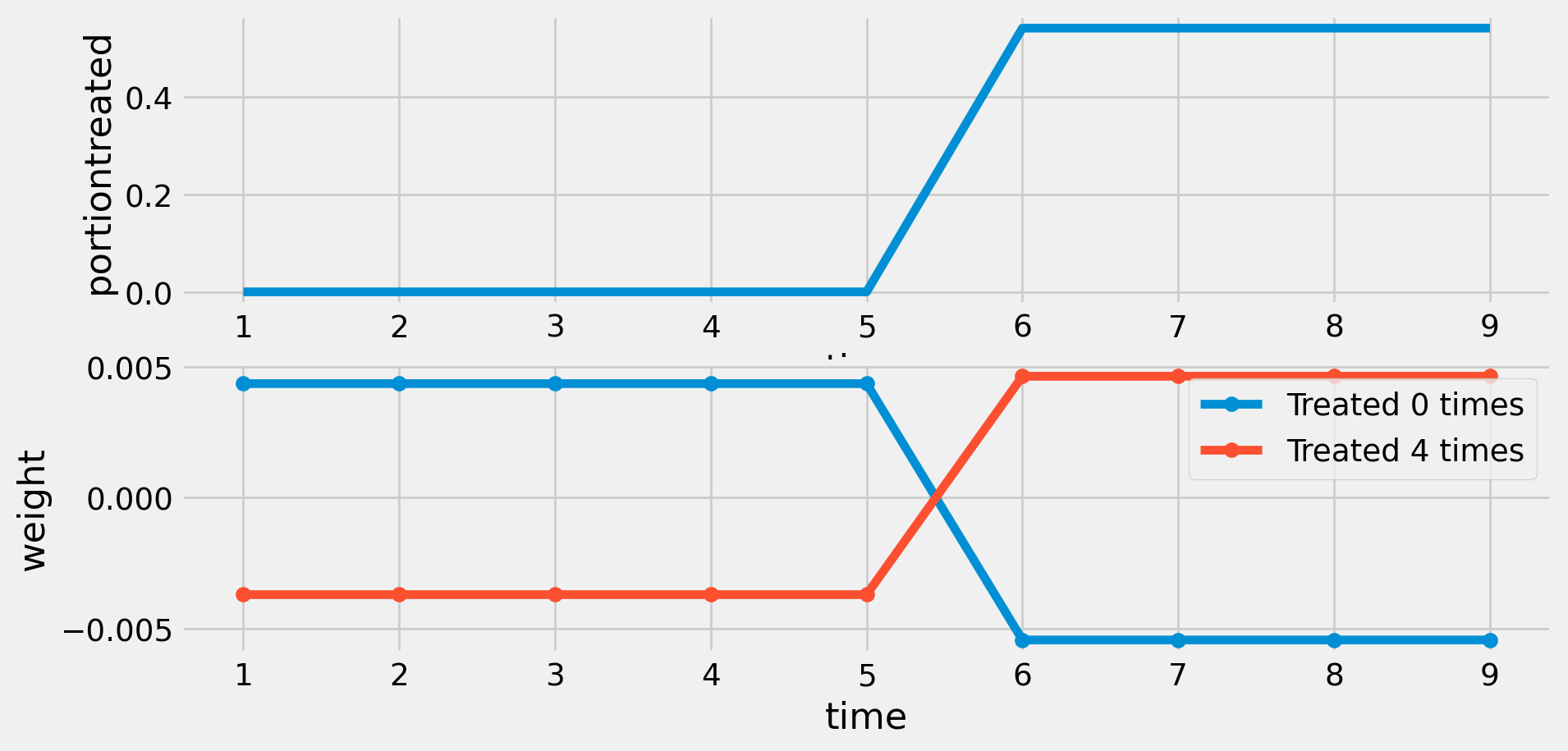
Distribution of Weights with a Single Treatment Time
Code
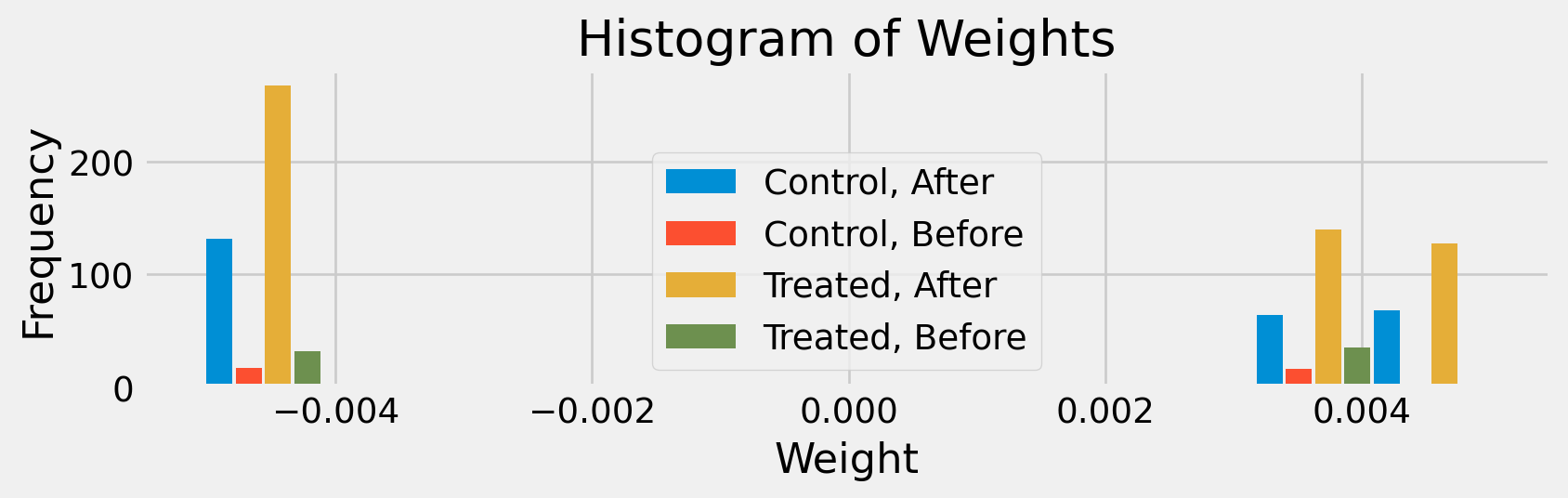
def histweights(D, ω=weights(D)):
"""
D: np.ndarray, shape (n, T), binary treatment indicators
ω: np.ndarray, shape (n, T), weights
"""
n, T = D.shape
# Ever treated per unit (row)
evertreated = np.any(D, axis=1) # shape (n,)
# After any treatment per time (column)
aftertreatment = np.any(D, axis=0) # shape (T,)
# Create group labels for each (unit, time) pair
g = []
for i in range(n):
for t in range(T):
et = evertreated[i]
at = aftertreatment[t]
label = ("Treated, " if et else "Control, ") + ("After" if at else "Before")
g.append(label)
# Flatten weights for histogram
ω_flat = ω.flatten()
# Plot grouped histogram
plt.figure(figsize=(9,3))
bins = np.histogram_bin_edges(ω_flat, bins='auto')
bin_width = np.diff(bins)[0]
bin_centers = bins[:-1] + bin_width / 2
unique_groups = sorted(set(g))
n_groups = len(unique_groups)
offsets = np.linspace(-bin_width/2, bin_width/2, n_groups, endpoint=False)
for idx, group in enumerate(unique_groups):
mask = np.array(g) == group
hist, _ = np.histogram(ω_flat[mask], bins=bins)
plt.bar(bin_centers + offsets[idx], hist, width=bin_width/(n_groups+0.5), label=group, align='center')
plt.title("Histogram of Weights")
plt.xlabel("Weight")
plt.ylabel("Frequency")
plt.legend()
plt.tight_layout()
plt.show()
histweights(D)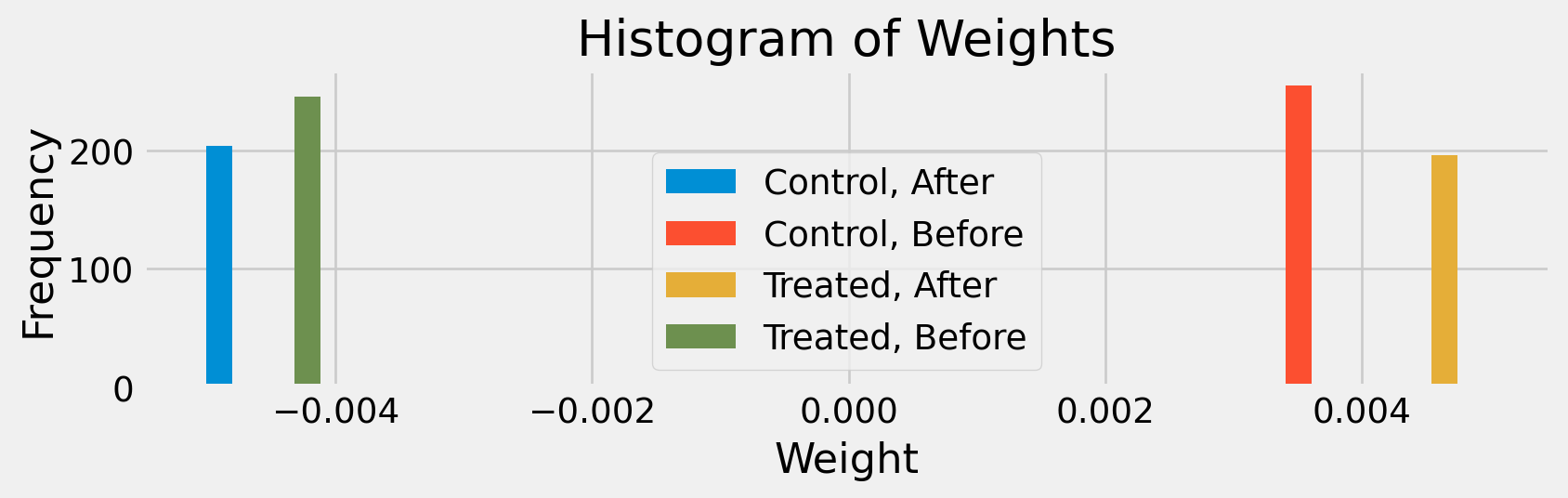
Weights with Early and Late Treated
Distribution of Weights with Early and Late Treated
Sign Reversal
Code
dvals = np.unique(D,axis=0)
dvals.sort()
ATT = np.ones(T)
ATT[0] = 0.0
ATT[T-2:T] = 6.0
np.random.seed(6798)
def simulate(n,T,pt,ATT,sigma=1.0):
D = assigntreat(n,T,pt)
y = np.random.randn(n,T)*sigma + ATT[np.cumsum(D, axis=1)]
df = pd.DataFrame({
'id': np.repeat(np.arange(1, n + 1), T),
't': np.tile(np.arange(1, T + 1), n),
'y': y.flatten(),
'D': D.flatten()
})
return(df)
df = simulate(n,T,pt,ATT)
result = pf.feols('y ~ D | id + t', df, vcov={"CRV1": "id"})
result.summary()###
Estimation: OLS
Dep. var.: y, Fixed effects: id + t
sample: None = all
Inference: CRV1
Observations: 900
| Coefficient | Estimate | Std. Error | t value | Pr(>|t|) | 2.5% | 97.5% |
|:--------------|-----------:|-------------:|----------:|-----------:|-------:|--------:|
| D | -0.526 | 0.251 | -2.096 | 0.039 | -1.023 | -0.028 |
---
RMSE: 1.287 R2: 0.51 R2 Within: 0.009 When to worry
- If multiple treatment times and treatment heterogeneity
- Even if weights do not have wrong sign, the fixed effects estimate is hard to interpret
- Same logic applies more generally – not just to time
- E.g. if have group effects, some treated units in multiple groups, and \(E[y(1) - y(0) | group]\) varies
What to Do?
- Follow identification \[
\begin{align*}
ATT_{t,t-s}& = \Er[y_{it} - y_{it-s} | D_{it}=1, D_{it-s}=0] - \Er[y_{it} - y_{it-s} | D_{it}=0, D_{it-s}=0]
\end{align*}
\] and estimate \[
\begin{align*}
\widehat{ATT}_{t,t-s} = & \frac{\sum_i y_{it} D_{it}(1-D_{it-s})}{\sum_i D_{it}(1-D_{it-s})} \\
& - \frac{\sum_i y_{it} (1-D_{it})(1-D_{it-s})}{\sum_i (1-D_{it})(1-D_{it-s})}
\end{align*}
\] and perhaps some average, e.g. (there are other reasonable weighted averages) \[
\sum_{t=1}^T \frac{\sum_i D_{it}}{\sum_{i,s} D_{i,s}} \frac{1}{t-1} \sum_{s=1}^{t-1} \widehat{ATT}_{t,t-s}
\]
- Code? Inference? Optimal? (could create it, but there’s an easier way)
What to Do?
- Option 1: Use an appropriate package
- pyfixest see especially their docs on difference in differences
- csdid
- doubleml (see chapter 16 of Chernozhukov et al. (2024))
- differences
- see https://asjadnaqvi.github.io/DiD/ for more options
What to Do?
Option 2: estimate a correctly specified fixed effects regression (my preferred approach)
Problem is possible correlation of \((y_{it}(1) - y_{it}(0))D_{it}\) with \(\tilde{D}_{it}\)
\(\tilde{D}_{it}\) is function of \(t\) and \((D_{i1}, ..., D_{iT})\)
Estimating separate coefficient for each combination of \(t\) and \((D_{i1}, ..., D_{iT})\) will eliminate correlation / flexibly model treatment effect heterogeneity
What to Do?
- Cohorts = unique sequences of \((D_{i1}, ..., D_{iT})\)
- In current simulated example, three cohorts
- \((0, 0, 0, 0, 0, 0, 0, 0, 0)\)
- \((0, 0, 0, 0, 0, 0, 0, 1, 1)\)
- \((0, 1, 1, 1, 1, 1, 1, 1, 1)\)
- In current simulated example, three cohorts
Regression with Cohort-time Interactions
Estimate: \[ y_{it} = \sum_{c=1}^C D_{it} 1\{C_i=c\} \beta_{ct} + \alpha_i + \delta_t + \epsilon_{it} \]
\(\hat{\beta}_{ct}\) consistently estimates \(\Er[y_{it}(1) - y_{it}(0) | C_{i}=c, D_{it}=1]\) assuming parallel trends holds for all periods \[ \Er[y_{it}(0) - y_{it-s}(0) | C_i=c] = \Er[y_{it}(0) - y_{it-s}(0) | C_i=c'] \] for all \(t, s, c, c'\)
Regression with Cohort Interactions
def definecohort(df):
# convert dummies into categorical
n = len(df.id.unique())
T = len(df.t.unique())
df = df.set_index(['id','t'])
dmat=np.array(df.sort_index().D)
dmat=np.array(df.D).reshape(n,T)
cohort=dmat.dot(1 << np.arange(dmat.shape[-1] - 1, -1, -1))
cdf = pd.DataFrame({"id":np.array(df.index.levels[0]), "cohort":pd.Categorical(cohort)})
cdf =cdf.set_index('id')
df = df.reset_index().set_index('id')
df=pd.merge(df, cdf, left_index=True, right_index=True)
df=df.reset_index()
return(df)
dfc = definecohort(df)
def defineinteractions(df):
df['dct'] = 'untreated'
df['dct'] = df.apply(lambda x: f"t{x['t']},c{x['cohort']}" if x['D'] else f"untreated", axis=1)
return(df)
dfc = defineinteractions(dfc)
modc = pf.feols("y ~ C(dct, Treatment('untreated')) | id + t", dfc, vcov={"CRV1": "id"})
pf.etable([modc], type="md")Regression with Cohort Interactions
| | ('y', '(1)') |
|:--------------------------|:---------------|
| ('coef', 'dct=t2,c255') | 0.524 |
| | (0.278) |
| ('coef', 'dct=t3,c255') | 0.761* |
| | (0.322) |
| ('coef', 'dct=t4,c255') | 0.820** |
| | (0.305) |
| ('coef', 'dct=t5,c255') | 0.880** |
| | (0.331) |
| ('coef', 'dct=t6,c255') | 0.458 |
| | (0.286) |
| ('coef', 'dct=t7,c255') | 0.624* |
| | (0.309) |
| ('coef', 'dct=t8,c255') | 5.242*** |
| | (0.411) |
| ('coef', 'dct=t8,c3') | 1.121*** |
| | (0.313) |
| ('coef', 'dct=t9,c255') | 5.693*** |
| | (0.356) |
| ('coef', 'dct=t9,c3') | 1.007*** |
| | (0.287) |
| ('fe', 'id') | - |
| ('fe', 't') | - |
| ('stats', 'Observations') | 900 |
| ('stats', 'R²') | 0.724 |Regression with Cohort Interactions
import re
def plotcohortatt(modc):
coef = modc.coef()
ci = modc.confint()
tcregex = re.compile(r".+t(\d+),c(\d+)]")
catt = pd.DataFrame(index=coef.index, columns=['t','c','att','yerr'])
for i in range(len(coef)):
m = tcregex.match(coef.index[i])
t,c = m.groups()
t=int(t)
c=int(c)
catt.loc[coef.index[i]] = [t,c,coef.iloc[i],np.abs(ci.iloc[i].iloc[0]-coef.iloc[i])]
catt.sort_values(['c','t'],inplace=True)
fig, ax = plt.subplots()
ax.set(xlabel='time', ylabel='ATT | cohort')
for g in catt.groupby('c') :
c = g[0]
g = g[1]
ax.errorbar(g['t'], g['att'], yerr=g['yerr'], fmt='o', label=f'cohort {c}')
ax.legend()
return(fig)
fig=plotcohortatt(modc)Regression with Cohort Interactions
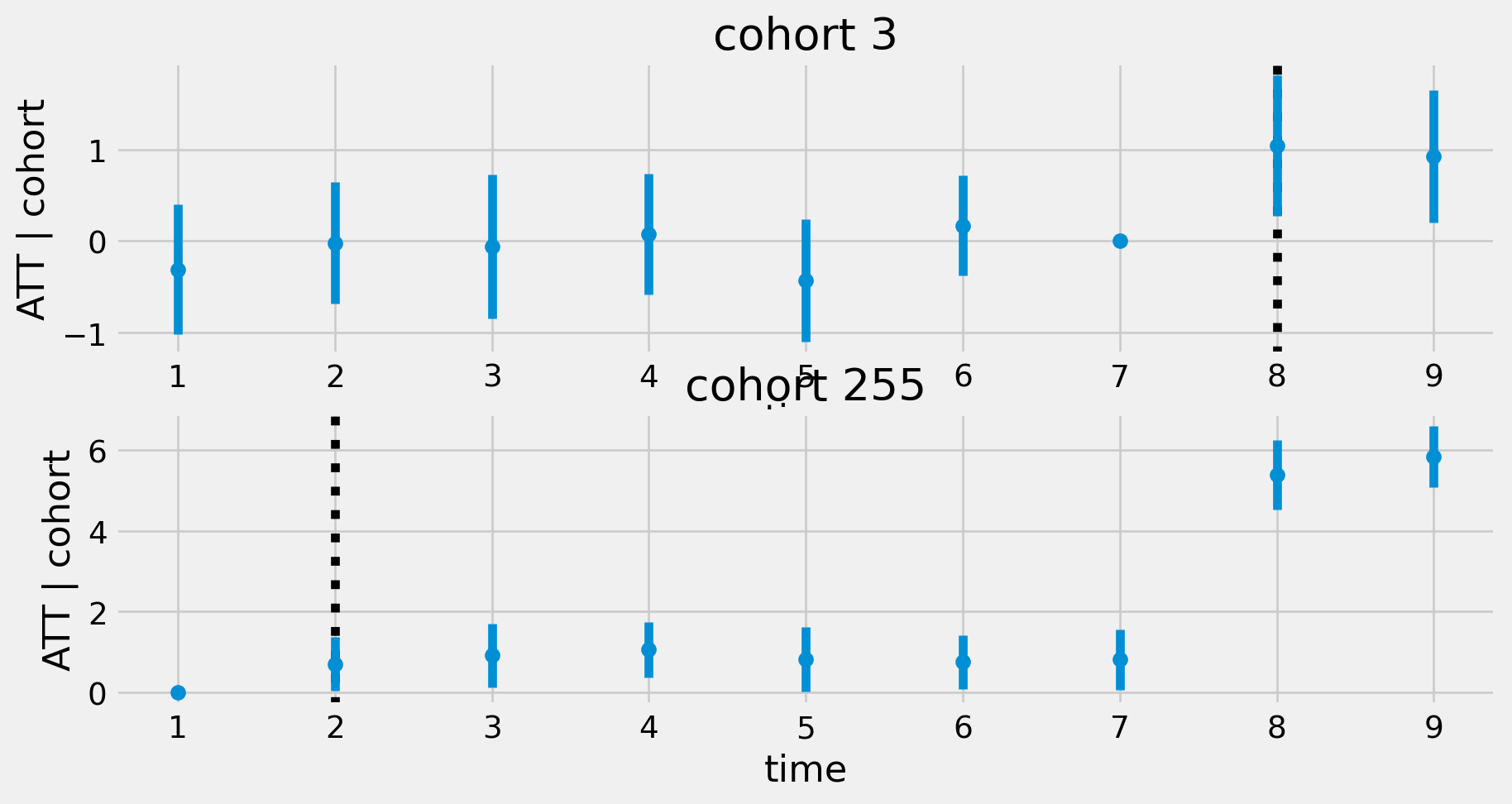
Regression with Cohort-Time Interactions
If just want to assume parallel trends for treated and never treated, i.e. \[ \Er[y_{it}(0) - y_{it-s}(0) | C_i=c] = \Er[y_{it}(0) - y_{it-s}(0) | C_i=c'] \] when \(c\) treated at \(t\), untreated at \(t-s\) and \(c'\) never treated
Estimate \[ y_{it} = \sum_{c=1}^C 1\{C_i=c\} \delta_{c,t} + \alpha_i + \epsilon_{it} \]
Regression with Cohort-Time Interactions
\[ y_{it} = \sum_{c=1}^C 1\{C_i=c\} \delta_{c,t} + \alpha_i + \epsilon_{it} \]
- \(\hat{\delta}_{c,t} + \frac{\sum \alpha_i 1\{C_i=c\}}{\sum 1\{C_i = c\}}\) consistently estimates \(\Er[y_{it} | C_{i} = c]\)
- \(\hat{\delta}_{c,t} -\hat{\delta}_{c,t-s}\) consistently estimates \(\Er[y_{it} - y_{i,t-s}| C_{i} = c]\)
- If \(c\) treated at \(t\), not at \(t-s\), and \(c'\) not treated at either and assume parallel trends, \[ \hat{\delta}_{c,t} - \hat{\delta}_{c,t-s} - (\hat{\delta}_{c',t} -\hat{\delta}_{c',t-s}) \inprob \Er[y_{it}(1)-y{it}(0)| C_i =c] \]
Regression with Cohort-Time Interactions
| | ('y', '(1)') |
|:-----------------------------|:---------------|
| ('coef', 'cohort=3 × t=2') | 0.288 |
| | (0.357) |
| ('coef', 'cohort=255 × t=2') | 0.696* |
| | (0.340) |
| ('coef', 'cohort=3 × t=3') | 0.248 |
| | (0.406) |
| ('coef', 'cohort=255 × t=3') | 0.909* |
| | (0.407) |
| ('coef', 'cohort=3 × t=4') | 0.386 |
| | (0.345) |
| ('coef', 'cohort=255 × t=4') | 1.051** |
| | (0.352) |
| ('coef', 'cohort=3 × t=5') | -0.119 |
| | (0.377) |
| ('coef', 'cohort=255 × t=5') | 0.809* |
| | (0.407) |
| ('coef', 'cohort=3 × t=6') | 0.480 |
| | (0.292) |
| ('coef', 'cohort=255 × t=6') | 0.745* |
| | (0.340) |
| ('coef', 'cohort=3 × t=7') | 0.309 |
| | (0.362) |
| ('coef', 'cohort=255 × t=7') | 0.808* |
| | (0.384) |
| ('coef', 'cohort=3 × t=8') | 1.349** |
| | (0.400) |
| ('coef', 'cohort=255 × t=8') | 5.378*** |
| | (0.440) |
| ('coef', 'cohort=3 × t=9') | 1.235** |
| | (0.385) |
| ('coef', 'cohort=255 × t=9') | 5.829*** |
| | (0.385) |
| ('fe', 'id') | - |
| ('fe', 't') | - |
| ('stats', 'Observations') | 900 |
| ('stats', 'R²') | 0.725 |Using pyfixest: Cohort by Time Estimates
Code
dfc['first_treat_time'] = (
dfc.groupby('id').apply(
lambda g: g.loc[g['D'] == 1, 't'].iloc[0] if (g['D'] == 1).any() else 0
).reindex(dfc['id']).values
)
fit_saturated = pf.event_study(
data=dfc,
yname="y",
idname="id",
tname="t",
gname="first_treat_time",
estimator="saturated",
)
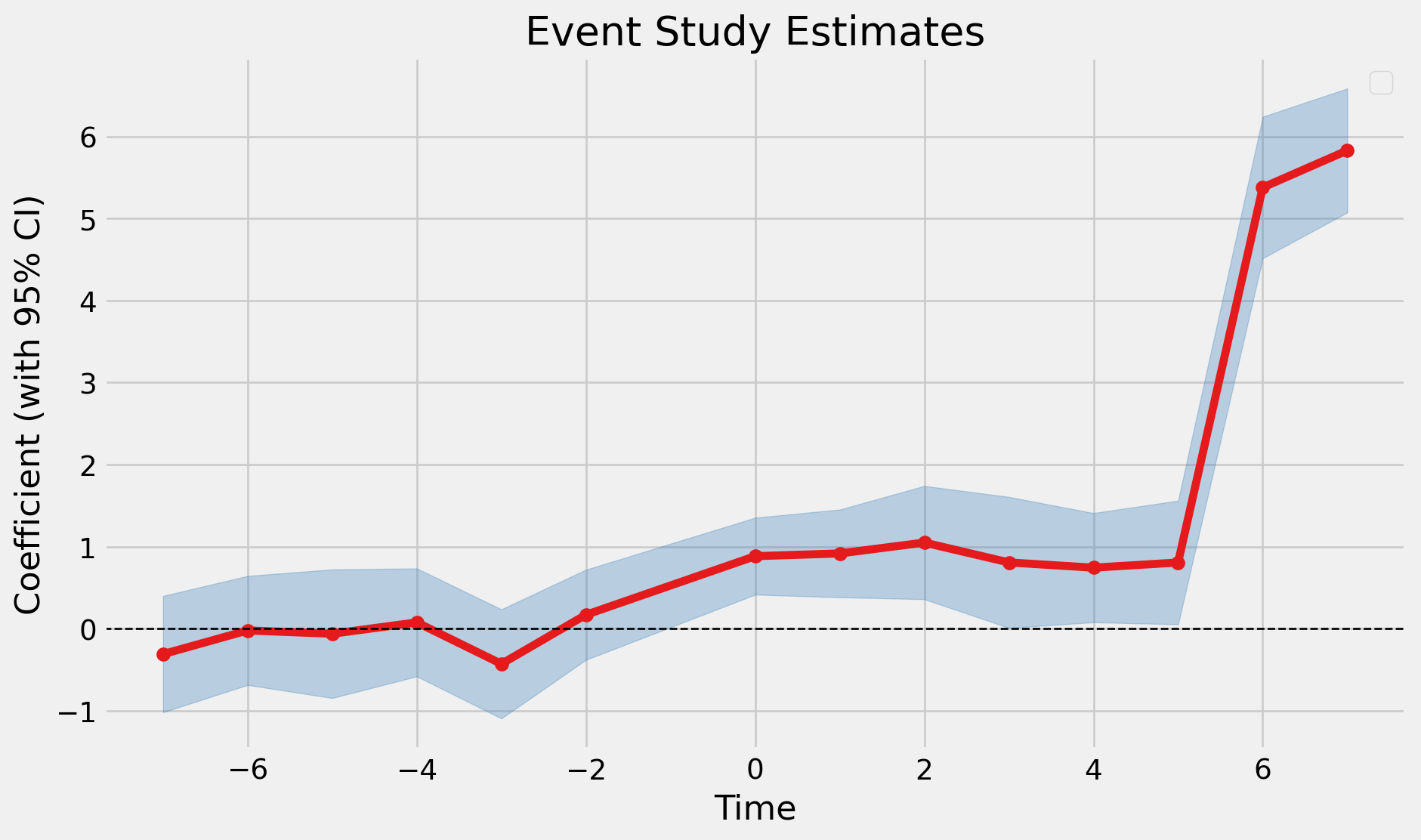
fit_saturated.iplot()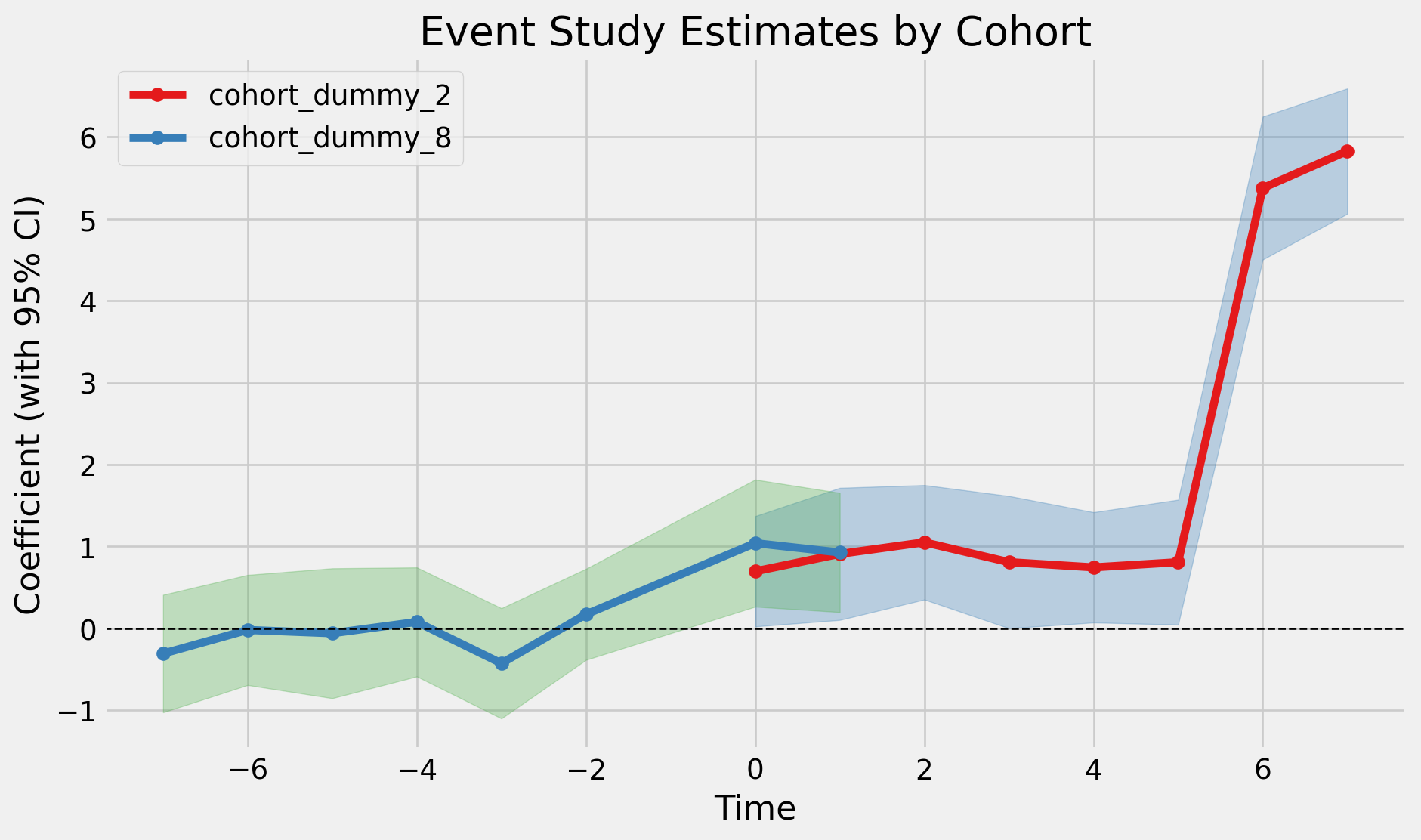
Using pyfixest: Aggregating Cohorts
Pre-Trends
Pre-trends
- Parallel trends assumption
\[ \Er[\color{red}{y_{it}(0)} - y_{it-s}(0) | D_{it}=1, D_{it-s}=0] = \Er[y_{it}(0) - y_{it-s}(0) | D_{it}=0, D_{it-s}=0] \]
- More plausible if there are parallel pre-trends
\[ \begin{align*} & \Er[y_{it-r}(0) - y_{it-s}(0) | D_{it}=1, D_{it-r}=0, D_{it-s}=0] = \\ & = \Er[y_{it-r}(0) - y_{it-s}(0) | D_{it}=0, D_{it-r}=0, D_{it-s}=0] \end{align*} \]
- Always at least plot pre-trends
Pre-trends
def eventstudyplot(modct) :
evdf = pd.DataFrame(index=modct.coef().index, columns=['c', 't','delta','did','se','vindex'])
pattern=r".+T\.(\d+).+\[T\.(\d+)\]"
for i in range(len(modct.coef())):
m = re.match(pattern, modct.coef().index[i])
c,t = m.groups()
t = int(t)
c = int(c)
evdf.loc[modct.coef().index[i]] = [c,t,modct.coef().iloc[i],0, 0, i]
evdf.sort_values(['c','t'],inplace=True)
T = evdf['t'].max()
V = modct._vcov
evdf.reset_index(inplace=True)
for t in range(T) :
if not (t+1) in evdf.t.unique() :
ndf = pd.DataFrame(columns=evdf.columns)
ndf.c=evdf.c.unique()
ndf.t=t+1
ndf.delta=0
ndf.vindex=V.shape[0]
evdf=pd.concat([evdf,ndf])
V = np.vstack([V,np.zeros(V.shape[1])])
V = np.hstack([V,np.zeros((V.shape[0],1))])
def did(g) :
c = g.name
timestreated = bin(c).count('1')
t0 = T - timestreated
g=g.set_index('t')
g['did'] = g['delta'] - g['delta'][t0]
vi = g['vindex'].to_numpy().astype(int)
g['se'] = np.sqrt(V[vi,vi] - 2*V[g['vindex'][t0],vi] + V[g['vindex'][t0],g['vindex'][t0]])
return(g)
evdf=evdf.groupby('c').apply(did).reset_index()
fig, ax = plt.subplots(len(evdf.c.unique()),1)
for (i,g) in enumerate(evdf.groupby('c')) :
c = g[0]
g = g[1]
timestreated = bin(c).count('1')
t0 = T - timestreated + 1
ax[i].axvline(t0, color='black', ls=":")
ax[i].errorbar(g['t'], g['did'], yerr=1.96*g['se'], fmt='o', label=f'cohort {c}')
ax[i].set_title(f'cohort {c}')
ax[i].set(xlabel='time', ylabel='ATT | cohort')
return(fig)
fig=eventstudyplot(modct)Pre-trends
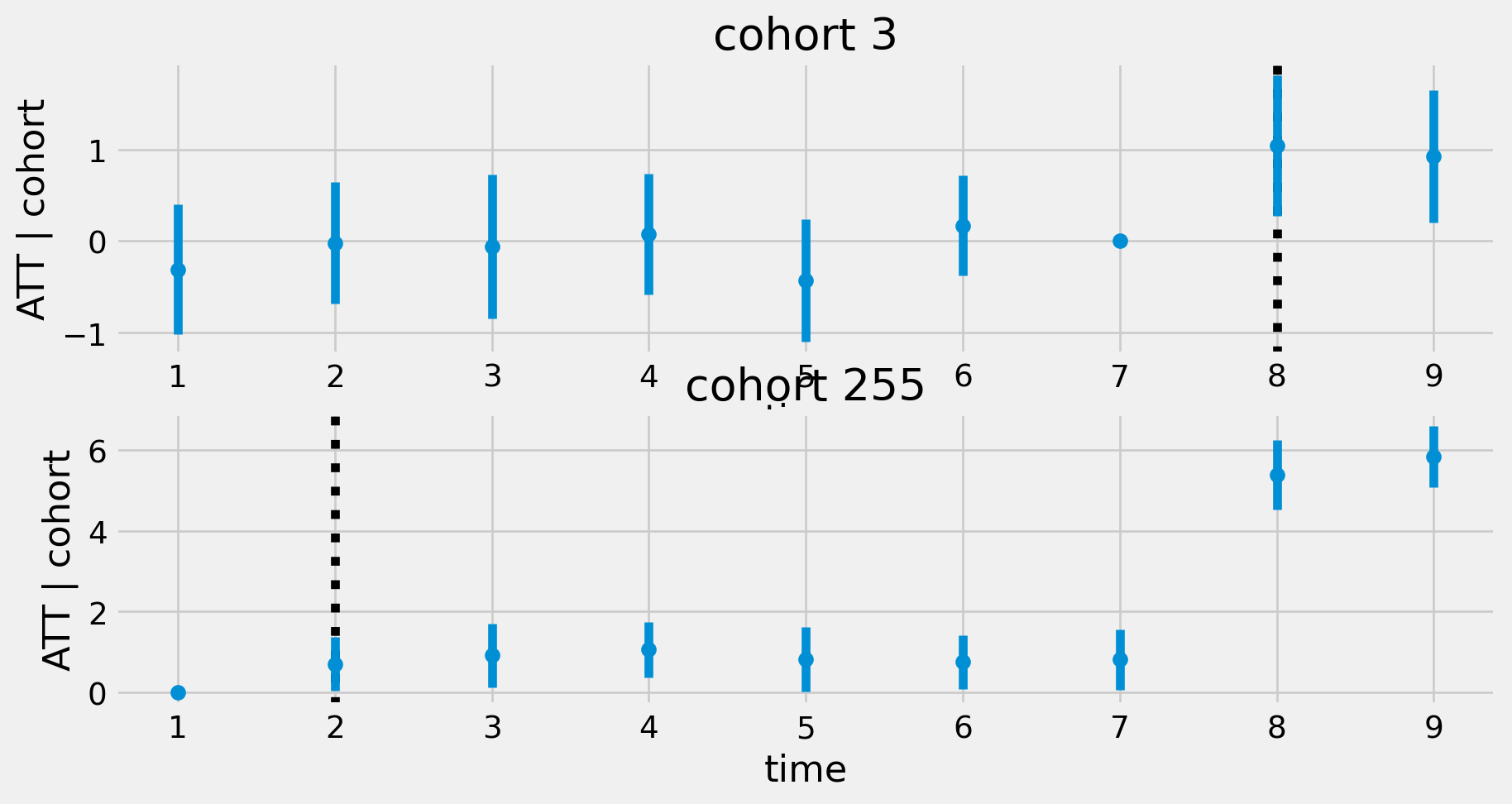
Testing for Pre-trends
- Is it a good idea to test
\[ \begin{align*} H_0 : & \Er[y_{it-r} - y_{it-s} | D_{it}=1, D_{it-r}=0, D_{it-s}=0] = \\ & = \Er[y_{it-r} - y_{it-s} | D_{it}=0, D_{it-r}=0, D_{it-s}=0]? \end{align*} \] - Even if not testing formally, we do it informally by plotting
Testing for Pre-trends
Distribution of \(\hat{ATT}\) conditional on fail to reject parallel pre-trends is not normal
Roth (2022) : test can have low power, and in plausible violations, \(\widehat{ATT}_{3,2}\) conditional on failing to reject is biased
Bounds from Pre-trends
Let \(\Delta\) be violation of parallel trends \[ \Delta = \Er[\color{red}{y_{it}(0)} - y_{it-1}(0) | D_{it}=1, D_{it-1}=0] - \Er[y_{it}(0) - y_{it-1}(0) | D_{it}=0, D_{it-1}=0] \]
Assume \(\Delta\) is bounded by deviation from parallel of pre-trends \[ |\Delta| \leq M \max_{r} \left\vert \tau^{1t}_{t-r,t-r-1} - \tau^{0t}_{t-r,t-r-1} \right\vert \] for some chosen \(M\)
See Rambachan and Roth (2023)
Covariates
Doubly Robust Difference in Differences
Sources and Further Reading
- Facure (2022, chap. 1)
- Huntington-Klein (2021, chap. 16)
- Book: Chaisemartin and D’Haultfœuille (2023)
- Recent reviews: Roth et al. (2023), Chaisemartin and D’Haultfœuille (2022), Arkhangelsky and Imbens (2023)
- Early work pointing to problems with fixed effects:
- Explosion of papers written just before 2020, published just after:
References
Arkhangelsky, Dmitry, and Guido Imbens. 2023. Causal Models for Longitudinal and Panel Data: A Survey.
Borusyak, Kirill, and Xavier Jaravel. 2018. Revisiting Event Study Designs. https://scholar.harvard.edu/files/borusyak/files/borusyak_jaravel_event_studies.pdf.
Callaway, Brantly, and Pedro H. C. Sant’Anna. 2021. “Difference-in-Differences with Multiple Time Periods.” Journal of Econometrics 225 (2): 200–230. https://doi.org/https://doi.org/10.1016/j.jeconom.2020.12.001.
Chaisemartin, C de, and X D’Haultfœuille. 2023. Credible Answers to Hard Questions: Differences-in-Differences for Natural Experiments. https://dx.doi.org/10.2139/ssrn.4487202.
Chaisemartin, Clément de, and Xavier D’Haultfœuille. 2020. “Two-Way Fixed Effects Estimators with Heterogeneous Treatment Effects.” American Economic Review 110 (9): 2964–96. https://doi.org/10.1257/aer.20181169.
Chaisemartin, Clément de, and Xavier D’Haultfœuille. 2022. “Two-way fixed effects and differences-in-differences with heterogeneous treatment effects: a survey.” The Econometrics Journal 26 (3): C1–30. https://doi.org/10.1093/ectj/utac017.
Chernozhukov, V., C. Hansen, N. Kallus, M. Spindler, and V. Syrgkanis. 2024. Applied Causal Inference Powered by ML and AI. https://causalml-book.org/.
Facure, Matheus. 2022. Causal Inference for the Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.
Goodman-Bacon, Andrew. 2021. “Difference-in-Differences with Variation in Treatment Timing.” Journal of Econometrics 225 (2): 254–77. https://doi.org/https://doi.org/10.1016/j.jeconom.2021.03.014.
Huntington-Klein, Nick. 2021. The Effect: An Introduction to Research Design and Causality. CRC Press. https://theeffectbook.net/.
Laporte, Audrey, and Frank Windmeijer. 2005. “Estimation of Panel Data Models with Binary Indicators When Treatment Effects Are Not Constant over Time.” Economics Letters 88 (3): 389–96. https://doi.org/https://doi.org/10.1016/j.econlet.2005.04.002.
Rambachan, Ashesh, and Jonathan Roth. 2023. “A More Credible Approach to Parallel Trends.” The Review of Economic Studies 90 (5): 2555–91. https://doi.org/10.1093/restud/rdad018.
Roth, Jonathan. 2022. “Pretest with Caution: Event-Study Estimates After Testing for Parallel Trends.” American Economic Review: Insights 4 (3): 305–22. https://doi.org/10.1257/aeri.20210236.
Roth, Jonathan, Pedro H. C. Sant’Anna, Alyssa Bilinski, and John Poe. 2023. “What’s Trending in Difference-in-Differences? A Synthesis of the Recent Econometrics Literature.” Journal of Econometrics 235 (2): 2218–44. https://doi.org/https://doi.org/10.1016/j.jeconom.2023.03.008.
Sant’Anna, Pedro H. C., and Jun Zhao. 2020. “Doubly Robust Difference-in-Differences Estimators.” Journal of Econometrics 219 (1): 101–22. https://doi.org/https://doi.org/10.1016/j.jeconom.2020.06.003.
Sun, Liyang, and Sarah Abraham. 2021. “Estimating Dynamic Treatment Effects in Event Studies with Heterogeneous Treatment Effects.” Journal of Econometrics 225 (2): 175–99. https://doi.org/https://doi.org/10.1016/j.jeconom.2020.09.006.
Wooldridge, Jeffrey M. 2005. “Fixed-Effects and Related Estimators for Correlated Random-Coefficient and Treatment-Effect Panel Data Models.” The Review of Economics and Statistics 87 (2): 385–90. https://doi.org/10.1162/0034653053970320.